Giá trị cực tiểu y C T của hàm số y = x 3 − 3 x 2 + 4 là
A. y C T = 0
B. y C T = 1
C. y C T = 4
D. y C T = 2
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
Cho hàm số y = a x 3 + b x 2 + c x + d đạt cực đại tại x = -2 với giá trị cực đại là 64; đạt cực tiểu tại x = 3 với giá trị cực tiểu là -61. Khi đó giá trị của a + b + c + d bằng
A. 1
B. 7
C. -17
D. 5
Ta có 64 = -8a + 4b - 2c + d; -61 = 27a + 9b + 3c +d
Từ y ' = 3 a x 2 + 2 b x + c ta thu được hai phương trình 0 = 12a - 4b + c; 0 = 27a + 6b + c
Giải hệ gồm 4 phương trình trên ta thu được a = 2; b = -3; c = -36; d = 20 hay a + b + c + d = -17
Đáp án C
Giá trị cực tiểu y C T của hàm số y = x + 4 x - 3 là:
A . y C T = - 3
B . y C T = - 1
C . y C T = 3
D . y C T = 1
Giá trị cực tiểu y C T của hàm số y = x + 4 x - 3 là.
A. y C T = -3
B. y C T = -1
C. y C T = 3
D. y C T = 1
Giá trị cực tiểu y C T của hàm số y = x + 4 x - 3 là
A. -3
B. -1
C. 3
D. 1
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Giá trị cực tiểu của hàm số y= x^3 -3x^2 -9x+2 là
A. -25
B. 3
C. 7
D. -20
Bài 4: Tìm giá trị của tham số m để hàm số: a) y=mx3 +mx2 −x+1 có cực đại, cực tiểu. b) y=x4 +(m−1)x2+1 có 3 cực trị.
Cho hàm số y = x 3 + 2 m x 2 + m 2 x - 3 Với giá trị nào của m thì hàm số đạt cực tiểu tại x = 1
A. m = - 1
B. m = - 3
C. m = - 1 hoặc m = - 3
D. không có giá trị nào của m
Đáp án A
Ta có: y’ = 3 x 2 + 4 m x + m 2
Hàm số đạt cực tiểu tại x = 1
⇒ y’(1) = 0
⇒ m = -3 hoặc m = -1
Với m = -3, ta có:
y’ = 0 ⇔ x = 1 hoặc x = 3
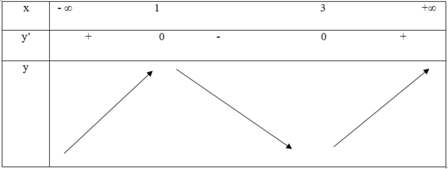
Vậy m = -3 không thoản mãn yêu cầu bài toán
Với m = -1, ta có:
y’ = 0 ⇔ x = 1 hoặc x = 1 3
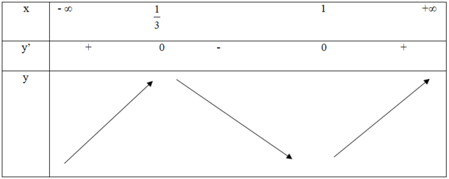
Vậy m = -1 thỏa mãn yêu cầu bài toán
Giá trị cực tiểu của hàm số y = e x x 2 − 3 là:
A. 6/e
B. 6 e 3
C. -3e
D. -2e
Đáp án D
Ta có y ' = e x x 2 − 3 + 2 x e x = e x x 2 + 2 x − 3 = 0 ⇔ x = 1 x = − 3
y ' ' = e x x 2 + 2 x − 3 + e x 2 x + 2 = e x x 2 + 4 x − 1
y ' ' − 3 = − 4 e − 3 < 0 ⇒ x = − 3 là điểm cực đại;
y ' ' 1 = 4 e > 0 ⇒ x = 1 là điểm cực tiểu ⇒ giá trị cực tiểu là y 1 = − 2 e