Cho hai số dương a, b với a khác 1. Mệnh đề nào dưới đây sai
A. log a 1 b = - log a b
B. log a b n = 1 n log a b
C. a log a b = a
D. log a a b = 1 - log a b
Cho bốn số thực dương a, b, x, y với \(a,b \ne 1\). Khẳng định nào sau đây là sai?
A. \({\log _a}(xy) = {\log _a}x + {\log _b}y\).
B. \({\log _a}\frac{x}{y} = {\log _a}x - {\log _a}y\).
C. \({\log _a}\frac{1}{x} = \frac{1}{{{{\log }_a}x}}\).
D. \({\log _a}b \cdot {\log _b}x = {\log _a}x\).
Cho hai số dương a, b với a ≠ 1 . Mệnh đề nào dưới đây sai?
A. log a 1 b = - log a b
B. log a b n = 1 n log a b
C. a log a b = a
D. log a a b = 1 - log a b
Chọn C
Phương pháp: dùng công thức logarit
Cách giải:
Mệnh đề A đúng
Mệnh đề B đúng vì b là số dương nên

Cho hai số thực dương a, b với \(a \ne 1\). Khẳng định nào sau đây là đúng?
A. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + {\log _a}b\).
B. \({\log _a}\left( {{a^3}{b^2}} \right) = 3 + 2{\log _a}b\).
C. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{3}{2} + {\log _a}b\).
D. \({\log _a}\left( {{a^3}{b^2}} \right) = \frac{1}{3} + \frac{1}{2}{\log _a}b\).
\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B
Cho hai số dương a , b ( a ≠ 1 ) . Mệnh đề nào dưới đây sai?
A. log a a α = α
B. a log a b = b
C. log a a = 2 a
D. log a 1 = 0
Cho hai số dương a, b a ≠ 1 . Mệnh đề nào dưới đây sai:
A. log a a α = α
B. a log a b = b
C. log a b = 2 a
D. log a 1 = 0
Cho hai số dương a, b (a≠1) Mệnh đề nào dưới đây SAI
A. log a a = 2 a
B. log a a α = α
C. log a 1 = 0
D. a log a b = b
Với a, b, c là các số thực dương khác 1, mệnh đề nào dưới đây sai?
A. log a b = log b log a
B. log a b = log c a log c b
C. log a b = 1 log b a
D. log a b = ln b ln a
Cho đồ thị ba hàm số \(y = {\log _a}x,y = {\log _b}x\) và \(y = {\log _c}x\) như hình bên. Mệnh đề nào sau đây là đúng?
A. \(a > b > c\).
B. \(b > a > c\).
C. \(a > b > c\).
D. \(b > c > a\).
Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)
\(log_cx\) nghịch biến biến nên 0<c<1
\(log_ax;log_bx\) đồng biến nên a>1; b>1
=>Loại D
\(log_ax>log_bx\left(x>1\right)\)
=>\(\dfrac{1}{log_xa}< \dfrac{1}{log_xb}\)
=>a<b
=>Chọn B
Cho ba số thực dương a, b, c khác 1 và đồ thị của ba hàm số lôgarit \(y = {\log _a}x;\,y = {\log _b}x;\,y = {\log _c}x\) được cho bởi Hình 15. Kết luận nào sau đây là đúng với ba số a, b, c?
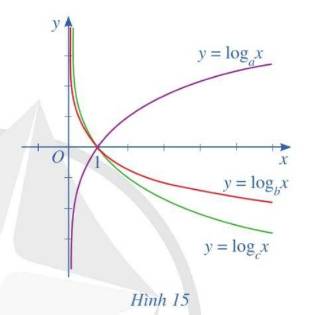
A. c < a < b
B. c < b < a
C. a < b < c
D. b < c < a