Nghiệm của phương trình sin2x+cosx=0 là
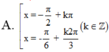
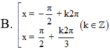
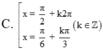
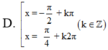
nghiệm của phương trình \(\dfrac{sin2x-1}{\sqrt{2}cosx-1}=0\) là
ĐK: \(x\ne\pm\dfrac{\pi}{4}+k2\pi\)
\(\dfrac{sin2x-1}{\sqrt{2}cosx-1}=0\)
\(\Leftrightarrow sin2x-1=0\)
\(\Leftrightarrow sin2x=1\)
\(\Leftrightarrow2x=\dfrac{\pi}{2}+k2\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+k\pi\)
Đối chiếu điều kiên ta được \(x=\pm\dfrac{3\pi}{4}+k2\pi\)
Số nghiệm của phương trình sin2x-cos2x=3sinx+cosx-2 thuộc ( 0 ; π 2 ) là:
A. 1
B. 2
C. 3
D. 4
Số nghiệm của phương trình sin2x-cos2x = 3sinx+cosx-2 thuộc 0 ; π 2 là:
A. 1.
B. 2.
C. 3.
D. 4
Tổng tất cả các nghiệm của phương trình sin2x/ cosx -1 =0 thuộc đoạn [0;2π ] là
Tìm số nghiệm thuộc khoảng - π ; π của phương trình cosx + sin2x = 0
A. 4
B. 3
C. 1
D. 2
Đáp án A
Ta có c o s x + sin 2 x = 0 ⇔ cos x + 2 sin x cos x = 0 ⇔ [ cos x = 0 sin x = - 1 2 ⇔ [ x = π 2 + k π x = - π 6 + k 2 π x = 7 π 6 + k 2 π
Mà x ∈ - π ; π ⇒ x ∈ - π 2 ; π 2 ; - π 6 ; - 5 π 6 .
Tìm nghiệm dương nhỏ nhất của phương trình: sin2x + cos2x + 3sinx – cosx – 2 = 0
A: π 3
B: π 6
C: π 12
D: 5 π 12
Một họ nghiệm của phương trình – 3sinx. cosx + sin2x = 2 là
![]()
![]()
![]()
![]()
Hướng dẫn giải:
Chọn A.
![]() không là nghiệm của phương trình
không là nghiệm của phương trình
Chia 2 vế phương trình cho cos2x ta được - 3tanx + tan2x = 2(1+ tan2x)
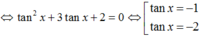
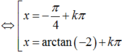
Cho phương trình: cosx+sinx=1+sin2x+cos2x. Nghiệm của phương trình có dạng x 1 = a π + k π x 2 = ± b π + k 2 π b > 0 . Tính tổng a + b
A. 1 12
B.3
C. 7 π 12
D. π 4
Phương trình sin 2 x + cos x = 0 có tổng các nghiệm trong khoảng 0 ; 2 π bằng
A. 2 π
B. 3 π
C. 5 π
D. 6 π
Đáp án là C.
p t ⇔ cos x 2 sin x + 1 = 0 ⇔ cos x = 0 sin x = − 1 2 ⇔ x = π 2 + k π x = − π 6 + k 2 π x = 7 π 6 + k 2 π ; k ∈ ℤ
x ∈ 0 ; 2 π ⇒ x ∈ π 2 ; 3 π 2 ; − π 6 ; 7 π 6 .
Tổng các nghiệm 5 π