Phương trình sin2x.cosx = sin7x.cos4x có nghiệm là:
A. ![]()
B. 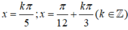
C. 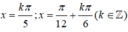
D. ![]()
Giải phương trình sin 2 x . cos x = sin 7 x . c o s 4 x .
A. x = k π 5 hoặc x = - π 12 + k π 6 k ∈ ℤ
B. x = k π 5 hoặc x = π 12 + k π 6 k ∈ ℤ
C. x = k π hoặc x = π 12 + k π 6 k ∈ ℤ
D. x = k π 5 hoặc x = - π 12 + k π k ∈ ℤ
Tìm nghiệm của các phương trình sau
a) \(2\left(sin2x.cosx-sinx.cos2x\right)-1=0\) (k thuoc Z)
b) \(\left(sin2x.cosx+sinx.cos2x\right)+2sin\frac{3x}{2}.cos\frac{3x}{2}-\sqrt{2}=0\)
a/ \(\Leftrightarrow2sin\left(2x-x\right)-1=0\)
\(\Leftrightarrow2sinx-1=0\Rightarrow sinx=\frac{1}{2}=sin\left(\frac{\pi}{6}\right)\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{6}+k2\pi\\x=\frac{5\pi}{6}+k2\pi\end{matrix}\right.\)
b/ \(\Leftrightarrow sin\left(2x+x\right)+sin3x=\sqrt{2}\)
\(\Leftrightarrow2sin3x=\sqrt{2}\)
\(\Leftrightarrow sin3x=\frac{\sqrt{2}}{2}=sin\left(\frac{\pi}{4}\right)\)
\(\Rightarrow\left[{}\begin{matrix}3x=\frac{\pi}{4}+k2\pi\\3x=\frac{3\pi}{4}+k2\pi\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\frac{\pi}{12}+\frac{k2\pi}{3}\\x=\frac{\pi}{4}+\frac{k2\pi}{3}\end{matrix}\right.\)
Cho phương trình a( x + 2) - a mũ 2 - 2= 0, a là tham số. Tìm a để :
a, Phương trình đã cho nhận x = 3 là nghiệm
b, Phương trình đã cho có một nghiệm duy nhất là âm
c, Phương trình đã cho vô nghiệm
d, Phương trình đã cho vô số nghiệm
a. để phương trình nhận x=3 là nghiệm ta có
\(a\left(3+2\right)-a^2-2=0\Leftrightarrow a^2-5a+2=0\Leftrightarrow a=\frac{5\pm\sqrt{17}}{2}\)
b. Để phương trình có duy nhất 1 nghiệm âm ta có :
\(\hept{\begin{cases}a\ne0\\x=\frac{a^2-2a+2}{a}< 0\end{cases}\Leftrightarrow a< 0}\) do \(a^2-2a+2>0\forall a\)
c. Để phương trình đã cho vô nghiệm thì a=0
d. Phương trình đã cho không thể có vô số nghiệm thực.
Câu 3. Phương trình vô nghiệm có tập nghiệm là?
A. S = f B. S = 0 C. S = {0} D. S = {f}
Câu 4. Điều kiện xác định của phương trình là?
A. x ≠ 2 và B. x ≠ -2 và C. x ≠ -2 và x ≠ 3 D. x ≠ 2 và
Câu 5. Cho AB = 3cm, CD = 40cm. Tỉ số của hai đoạn thẳng AB và CD bằng?
A. B. C. D.
Giải phương trình: Sin2x.Cosx + √3cos3x= √3-cos2x.sinx
Câu 4. Phương trình ![]() có nghiệm là
có nghiệm là
A. ![]() . B.
. B. ![]() . C.
. C. ![]() . D.
. D. ![]() .
.
phương trình 5x-2=6x có nghiệm là
A,x=2 B,x=0 C,x=-2 D,x=2/9
Nếu a, b, c, d là các số thực khác 0, biết c và d là nghiệm của phương trình x 2 + a x + b = 0 và a, b là nghiệm của phương trình x 2 + c x + d = 0 thì
A. -2
B. 0
C. − 1 + 5 2
D. 2
c và d là nghiệm của phương trình:
x 2 + a x + b ⇒ ⇒ c + d = − a ( 1 ) c d = b ( 2 )
a, b là nghiệm của phương trình:
x 2 + c x + d = 0 ⇒ ⇒ a + b = − c ( 3 ) a b = d ( 4 )

Đáp án cần chọn là: A
Cho a, b, c, d là các số thực, trong đó a, c khác 0. Điều kiện của a, b, c, d để nghiệm của phương trình a x + b = 0 nhỏ hơn nghiệm của phương trình c x + d = 0 là:
A. b a > c d
B. b a > c d
C. b d > a c
D. b a > d c
Ta có: a x + b = 0 ⇔ x = - b a
Và c x + d = 0 ⇔ x = - d c
Theo giả thiết ta có: - b a < - d c ⇔ b a > d c
Cho phương trình ( a mũ 2 + mũ 2 + 3 ) x- 1 = a mũ 2 ( x -1 ) + 3ax, a là tham số. Tìm để:
a, Phương trình đã nhận x = -1 là nghiệm
b, Phương trình đã cho có một nghiệm duy nhất là dương
c, Phương trình đã cho vô nghiệm
d, Phương trình đã cho vô số nghiệm
32+1123+ \(x = {-b \pm \sqrt{b^2-4ac} \over 2a}gfdrrffhjxxojmu09\)