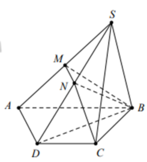
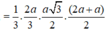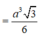Cho hình chóp S.ABCD có đáy ABCD là hình thang, AB//CD, AB=2CD. Gọi M N, tương ứng là trung điểm của SA và SD. Tính tỉ số V S . B C N M V S . B C D A
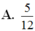
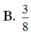
![]()
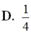
Cho hình chóp S.ABCD có đáy ABCD là hình thang, A B / / C D , A B =2 C D . Gọi M N, tương ứng là trung điểm của SA và SD. Tính tỉ số V S . B C N M V S . B C D A
A. 5 12
B. 3 8
C. 1 3
D. 1 4
Cho hình chóp S.ABCD có đáy ABCD là hình thang đáy AB, AB = 2DC. Gọi M, N là trung điểm của SA và SD. Tính tỉ số thể tích của hai hình chóp V S . B C M N V S . B C D A
A . 1 2
B . 5 12
C . 3 8
D . 1 3
Cho hình chóp S.ABCD có đáy ABCD là hình thang (AB // CD) và AB = 2CD. Gọi M, N lần lượt là trung điểm của các cạnh SA, SB. Chứng minh rằng:
a) MN // (SCD);
b) DM // (SBC);
c) Lấy điểm I thuộc cạnh SD sao cho`(SI)/(SD)=2/3`.Chứng minh rằng: SB // (AIC).
a) △SAB có: M, N là trung điểm của SA, SB nên MN // AB
Mà AB // CD
Suy ra MN // CD mà CD thuộc (SCD)
Do đó: MN // (SCD)
b) Ta có: MN = \(\dfrac{1}{2}\) AB
Mà CD = \(\dfrac{1}{2}\) AB
Suy ra: MN = CD mà MN // CD
Nên MNCD là hình bình hành. Do đó MD // CN
Mà CN thuộc (SBC)
Suy ra: DM // (SBC).
c) Gọi G là giao điểm của DM và AI; H là trung điểm của AB; O là giao điểm của AC và DH
Ta có: AHCD là hình bình hành vì AH // CD, AH = CD
Do đó: O là trung điểm của AC và DH
Ta chứng minh được G là trung điểm của DM
△DMH có: G, O là trung điểm của DM, DH
Suy ra: GO // MH
Mà MH // SB (M, H là trung điểm của SA, AB)
Do đó: GO // SB mà GO thuộc (AIC) nên SB // (AIC).
Cho hình chóp S.ABCD có đáy là hình thang, đáy lớn AB và AB= 2CD. Gọi I, J, K lần lượt là ba điểm trên các cạnh SA; AB; BC. Gọi F là giao điểm của SD và (IJK). Tính tỉ số F S F D
A. 1
B. 2
C. 1 2
D. 1 3
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB//CD, AB=2CD. Các cạnh bên có độ dài = 1. Gọi O là giao điểm của AC và BD. I là trung điểm của SO. Mặt phẳng \(\left(\alpha\right)\) thay đổi đi qua I và cắt SA,SB,SC,SD lần lượt tại M,N,P,Q. Tìm GTNN của biểu thức \(T=\dfrac{1}{2SM^2}+\dfrac{1}{2SN^2}+\dfrac{1}{SP^2}+\dfrac{1}{SQ^2}\)
Mọi người giúp mình với ạ!
Cho hình chóp S.ABCD, ABCD là hình thang, ab,cd là hai đáy có AB=2CD. Gọi M,N là trung điểm SA và AB. TÌM THIẾT DIỆN cắt bởi mp(MNC) và S.ABCD.
Cho hình chóp S.ABCDcó đáy ABCD là hình thang đáy AB,AB=2DC Gọi M, N là trung điểm của SA và SD. Tính tỉ số thể tích của hai hình chóp V S . B C N M V S . B C D A
A. 1 4
B. 5 12
C. 3 8
D. 1 3
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB=2a , BC=CD=AD=a Gọi M là trung điểm của AB. Biết SC = SD = SM và góc giữa cạnh bên SA và mặt phẳng đáy (ABCD) là 30 ° . Thể tích hình chóp đó là:
A. 3 a 3 6
B. 3 a 3 2
C. 3 3 a 3 2
D. 3 a 3 8
Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB = 2a, BC = CD = AD = a. Gọi M là trung điểm của AB. Biết SC = SD = SM và góc giữa cạnh bên SA và mặt phẳng đáy (ABCD) là 30 0 . Thể tích hình chóp đó là:
A . 3 a 3 6
B . 3 a 3 2
C . 3 3 a 3 2
D . 3 a 3 8
Đáp án A
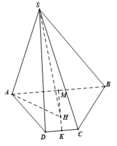
∆ DCM là tam giác đều cạnh a
=> SH ⊥ (ABCD) với H là tâm của ∆ DCM
Do đó (SA;(ABCD)) ![]()

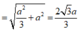
![]()
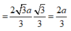
![]()