\(x^2-2xy+y^2+3x-3y-4=0\)

\(\Leftrightarrow\left(x-y\right)^2+3\left(x-y\right)-4=0\)

\(\Leftrightarrow\left(x-y\right)\left(x-y+3\right)-4=0\)

Thay y = 3 vào biểu thức trên ta được : 

\(x\left(x-3\right)-4=0\)

\(\Leftrightarrow x^2-3x-4=0\Leftrightarrow\left(x-4\right)\left(x+1\right)=0\Leftrightarrow x=4;x=-1\)

Vậy với y = 3 thì x = 4 ; x = -1 

Thay y = 3 vào bthuc ta được :

x² - 6x + 9 + 3x - 9 - 4 = 0

<=> x² - 3x - 4 = 0

<=> ( x + 1 )( x - 4 ) = 0

<=> x = -1 hoặc x = 4 

y'= \(4x^3-4\left(m-1\right)x\)

Để hàm số đồng biến trên khoảng (1;3) thì \(y'\left(x\right)\ge0,\forall x\in\left(1;3\right)\)

\(\Leftrightarrow x^2-\left(m-1\right)\ge0,\forall x\in\left(1;3\right)\)

\(\Leftrightarrow m-1\le x^2,\forall x\in\left(1;3\right)\)

\(\Rightarrow m-1\le1\Leftrightarrow m\le2\)

Vậy \(m\in\) (−\(\infty\);2]

Chọn C

Xét u =  x 2 + x + m  trên đoạn [-2;2] ta có 

Ta tính được u(-2) = m + 2; 

Nhận xét  nên 

Nếu 

Nếu 

Nếu 

Vậy tổng các giá trị thực của tham số là 

Chọn đáp án C.

Xét u = x 2 + x + m  trên đoạn [-2;2] ta có u ' = 0

Do đó

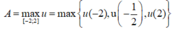
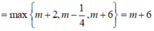
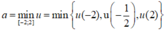
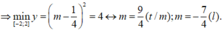
Vậy tổng các giá trị thực của tham số là  9 4 - 8 = - 23 4

Chọn A.

Tập xác định:D= R. Ta có:y ‘= m-3 + (2m+1).sinx

Hàm số nghịch biến trên R

Trường hợp 1: m= -1/ 2 ; ta có  0 ≤ 7 2   ∀ x ∈ ℝ

Vậy hàm số luôn nghịch biến trên R.

Trường hợp 2: m< -1/ 2 ; ta có

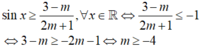
Trường hợp 3:m > -1/2 ; ta có:

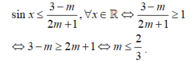
Vậy  - 4 ≤ m ≤ 2 3

Chứng minh công thức tổng quát phương trình đi qua 2 điểm cực trị:

giả sử hàm bậc 3: \(y=ax^3+bxx^2+cx+d\left(a\ne0\right)\) có 2 điểm cực trị x1;x2

Ta đi tìm số dư 1 cách tổng quát: 

Ta có: \(y'=3ax^2+2bx+c-và-y''=6ax+b\) 

Xét phép chia giữa y' và y'' ta có: \(y=y'\left(\dfrac{1}{3}x+\dfrac{b}{9a}\right)+g\left(x\right)\left(1\right)\) là phường trình đi qua 2 điểm cực trị của đồ thị hàm số bậc 3

từ (1) Ta có: \(y=y'\dfrac{3ax+b}{9a}+g\left(x\right)-hay-y=y'\dfrac{6ax+2b}{18a}g\left(x\right)\) 

Từ đây dễ suy ra: \(g\left(x\right)=y-\dfrac{y'.y''}{18a}\left(công-thức-tổng-quát\right)\) ( dĩ nhiên bạn chỉ cần nhớ cái này ) 

áp dụng vào bài toán ta có: 

\(2x^3+3\left(m-1\right)x^2+6m\left(1-2m\right)x-\left(6x^2+6\left(m-1\right)x+6m\left(1-2m\right)\right).\dfrac{12x+6\left(m-1\right)}{18.2}\)

Gán:  \(\left\{{}\begin{matrix}x=i\\m=10\end{matrix}\right.\) => 1710-841i

\(\Rightarrow y=4m\left(-2m-1\right)x+17m^2+m\) bài toán quay trở về bài toán đơn giản bạn giải nốt là oke