Cho (H) là hình phẳng nằm bên trong nửa elip y = 1 2 4 - x 2 và nằm bên ngoài parabol y = 3 2 x 2 Diện tích của (H) bằng
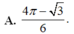
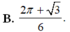
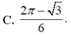
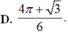
Cho (H) là hình phẳng nằm bên trong nửa elip y = 1 2 4 - x 2 và nằm bên ngoài parabol y = 3 2 x 2 Diện tích của (H) bằng
A. 4 π - 3 6
B. 2 π + 3 6
C. 2 π - 3 6
D. 4 π + 3 6
Cho (H) là hình phẳng nằm bên trong nửa elip y = 1 2 4 - x 2 và nằm bên ngoài parabol y = 3 2 x 2 . Diện tích của (H) bằng
A. 4 π - 3 6
B. 2 π + 3 6
C. 2 π - 3 6
D. 4 π + 3 6
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 2 x 2 và nửa đường elip có phương trình y = 1 2 4 - x 2 (với - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
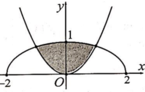
A. 2 π + 3 6
B. 2 π + 3 12
C. 2 π - 3 6
D. 4 π + 3 6
Chọn đáp án A
Phương trình hoành độ giao điểm của parabol y = 3 2 x 2 và nửa đường elip
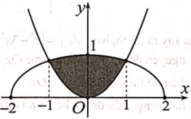
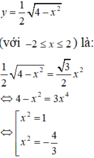
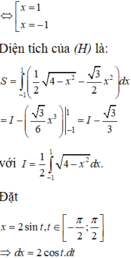
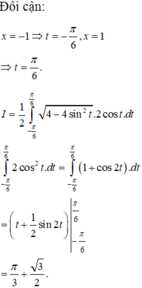
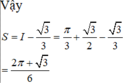
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 2 x 2 và nửa đường elip có phương trình y = 1 2 4 - x 2 ( v ớ i - 2 ≤ x ≤ 2 ) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
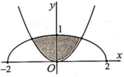
A. 2 π + 3 6
B. 2 π + 3 12
C. 2 π - 3 6
D. 4 π + 3 6
Trong bản vẽ thiết kế, vòm của ô thoáng trong Hình 7.22 là nửa nằm phía trên trục hoành của elip có phương trình \(\frac{{{x^2}}}{{16}} + \frac{{{y^2}}}{4} = 1\). Biết rằng 1 đơn vị trên mặt phẳng toạ độ của bản vẽ thiết kế ứng với 30 cm trên thực tế. Tinh chiều cao h của ô thoáng tại điểm cách điểm chính giữa của đế ô thoáng 75 cm.
75 cm trên bản vẽ ứng với 2,5 đơn vị trên mặt phẳng tọa độ.
Gọi M là điểm trên vòm ô thoáng, có hoành độ 2,5 và tung độ là h.
M thuộc elip nên \(\frac{{2,{5^2}}}{{16}} + \frac{{{h^2}}}{4} = 1\)
\(\Leftrightarrow h = \sqrt {4.\left( {1 - \frac{{2,{5^2}}}{{16}}} \right)} = \frac{{\sqrt {39} }}{4} \approx 1,56\)
Vậy độ cao h trên thực tế là: \(h = 1,56.30 = 46,8\) cm
Cho (H) là hình phẳng giới hạn bởi đường thẳng y = - 1 2 x + 1 và nửa đường elip có phương trình y = 1 2 4 - x 2 (với ) (phần tô đậm trong hình vẽ). Diện tích của (H) bằng:
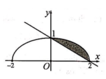
A. π - 1 4
B. π - 2 4
C. π + 1 2
D. π - 2 2
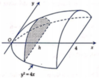
Một vật thể có mặt đáy nằm trong mặt phẳng tọa độ (Oxy) được giới hạn bởi đường cong y 2 = 4 x và đường thẳng x = 4. Thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox là một nửa hình elip có trục lớn gấp đôi trục nhỏ. Tính thể tích của vật thể.

A. 8 π
B. 16 π
C. 32 π
D. 64 π
Đáp án A
Xét thiết diện của vật thể cắt bởi mặt phẳng vuông góc với Ox tại điểm x là nửa elip có bán trục lớn bằng 2 x , do đó có bán trục nhỏ bằng x (do trục lớn gấp đôi trục nhỏ)
Suy ra diện tích của thiết diện tại điểm x là S x = 1 2 . π .2 x . x = π x
Vậy thiết diện của vật thể là V = ∫ 0 4 π x d x = π x 2 2 4 0 = 8 π . Chọn đáp án A
Một vật thể có mặt đáy nằm trong mặt phẳng tọa độ (Oxy) được giới hạn bởi đường cong y 2 = 4 x và đường thẳng x = 4. Thiết diện của vật thể cắt bởi mặt phẳng vuông góc với trục Ox là một nửa hình elip có trục lớn gấp đôi trục nhỏ. Tính thể tích của vật thể
A. 8 π
B. 16 π
C. 32 π
D. 64 π
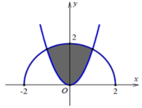
Cho (H) là hình phẳng giới hạn bởi parabol y = 3 x 2 và nửa đường tròn có phương trình y = 4 - x 2 với - 2 ≤ x ≤ 2 (phần tô đậm trong hình vẽ). Diện tích của (H) bằng
A. 2 π + 5 3 3
B. 4 π + 5 3 3
C. 4 π + 3 3
D. 2 π + 3 3
Chọn D.
Hoành độ giao điểm của (P) và ( C) là nghiệm của 3 x 2 = 4 - x 2 <=> x = 1 hoặc x = -1
Khi đó, diện tích cần tính là H = 2x ( ∫ 0 1 4 - x 2 d x - ∫ 0 1 3 x 2 d x ) = 2 π + 3 3