Đáp án B

giúp mình với

Chọn B.

+ Tính S:

Ta có nửa chu vi tam giác là p = (7 + 8 + 5) : 2 = 10

Suy ra: 

+ Tính góc A:

Ta có: 

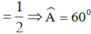
+ Tính AD:

Ta có: S_ABD= ½.AB. AD.sin(A/2) = ½.5.AD.sin30⁰ = 5/4 AD

S_ACD= ½AC. AD.sin(A/2) = ½.5.AD.sin30⁰ = 2AD

Mà: S = S_ABD+ S_ACD

Nên  hay  suy ra 

a)

– Tọa độ trọng tâm G của tam giác ABC là:

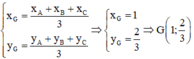
– Tọa độ trực tâm H của tam giác ABC:

Cách 1:

+ Phương trình đường cao BD:

BD ⊥ AC ⇒ Đường thẳng BD nhận 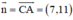 là một vtpt

BD đi qua B(2; 7)

⇒ Phương trình đường thẳng BD: 7(x - 2) +11(y - 7) = 0 hay 7x + 11y – 91 = 0

+ Phương trình đường cao CE:

CE ⊥ AB ⇒ Đường thẳng CE nhận 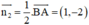 là một vtpt

CE đi qua C(–3; –8)

⇒ Phương trình đường thẳng CE: 1(x + 3) – 2(y + 8)=0 hay x – 2y – 13 = 0.

Trực tâm H là giao điểm của BD và CE nên tọa độ của H là nghiệm của hpt:

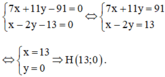
Cách 2: Gọi H(x, y) là trực tâm tam giác ABC

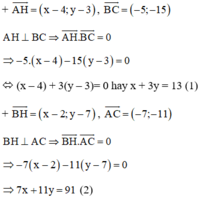
Từ (1) và (2) ta có hệ phương trình

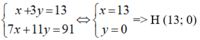
b) Gọi T(x; y) là tâm đường tròn ngoại tiếp tam giác ABC

Khi đó TA = TB = TC = R.

+ TA = TB ⇒ AT2 = BT2

⇒ (x – 4)2 + (y – 3)2 = (x – 2)2 + (y – 7)2

⇒ x2 – 8x + 16 + y2 – 6y + 9 = x2 – 4x + 4 + y2 – 14y + 49

⇒ 4x – 8y = –28

⇒ x – 2y = –7 (1)

+ TB = TC ⇒ TB2 = TC2

⇒ (x – 2)2 + (y – 7)2 = (x + 3)2 + (y + 8)2

⇒ x2 – 4x + 4 + y2 – 14y + 49 = x2 + 6x + 9 + y2 + 16y + 64

⇒ 10x + 30y = –20

⇒ x + 3y = –2 (2)

Từ (1) và (2) ⇒ x = –5, y = 1 ⇒ T(–5 ; 1).

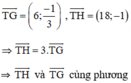
⇒ T, H, G thẳng hàng.

c) Tâm đường tròn ngoại tiếp ΔABC: T(–5; 1)

Bán kính đường tròn ngoại tiếp ΔABC:

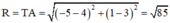
Vậy phương trình đường tròn ngoại tiếp tam giác ABC:

(x + 5)2 + (y – 1)2 = 85

Do G là trọng tâm tam giác ABC nên tọa độ G:

x G = x A + ​ x B + ​ x C 3 = − 1 + ​ 5 + ​ 0 3 = 4 3 y G = y A + ​ y B + ​ y C 3 = ​ 1 + ​ ( − 3 ) + 2 3 = 0 ⇒ G 4 3 ;    0

Điểm G1 là điểm đối xứng của G qua trục Oy nên  G 1 ​   − 4 3 ;    0

Đáp án D

câu a rất đơn giản, bạn tự làm nhé

b) xét tam giác ABC cân tại A có Ad lừ đường phân giác từ đỉnh => AD là trung tuyến ứng với BC 

mà G là trọng tâm của tam giác ABC => A,G,D thẳng hàng

c) vì tam giác abd= tam giác acd (câu a) => DB= DC( 2 cạnh tương ứng) => DB= 1/2 BC = 10cm/2 = 5cm

xét tam giác abc cân tại a có ad là trung tuyến ứng với cạnh đấy => ad là đường cáo ứng với cạnh đáy => ADB = 90^o

Áp dụng định lý Pytago cho tam giác ABD vuông tại D ta có AD² +DB² = AB²

                                                                                                ... bạn tự tính tiếp nhé =.> AD= 12cm

mà G là trọng tâm => DG = 1/3 AD

                                    DG= 12cm/3 = 4cm

vậy DG=4cm(dpcm)

câu a rất đơn giản, bạn tự làm nhé

b) xét tam giác ABC cân tại A có Ad lừ đường phân giác từ đỉnh => AD là trung tuyến ứng với BC 

mà G là trọng tâm của tam giác ABC => A,G,D thẳng hàng

c) vì tam giác abd= tam giác acd (câu a) => DB= DC( 2 cạnh tương ứng) => DB= 1/2 BC = 10cm/2 = 5cm

xét tam giác abc cân tại a có ad là trung tuyến ứng với cạnh đấy => ad là đường cáo ứng với cạnh đáy => ADB = 90^o

Áp dụng định lý Pytago cho tam giác ABD vuông tại D ta có AD² +DB² = AB²

                                                                                                ... bạn tự tính tiếp nhé =.> AD= 12cm

mà G là trọng tâm => DG = 1/3 AD

                                    DG= 12cm/3 = 4cm

vậy DG=4cm(dpcm)

Theo t/c đường tròn, do M là trung điểm BC \(\Rightarrow OM\perp BC\)

Áp dụng định lý Pitago:

\(OM=\sqrt{OC^2-CM^2}=\sqrt{R^2-\left(\dfrac{BC}{2}\right)^2}=3\)

\(\Rightarrow\) Quỹ tích M là đường tròn tâm \(\left(O;3\right)\)

Mặt khác do G là trọng tâm tam giác ABC

\(\Rightarrow\overrightarrow{AG}=\dfrac{2}{3}\overrightarrow{AM}\)

\(\Rightarrow\) G là ảnh của M qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)

\(\Rightarrow\) Quỹ tích G là ảnh của \(\left(O;3\right)\) qua phép vị tự tâm A tỉ số \(k=\dfrac{2}{3}\)

\(\Rightarrow\) Quỹ tích G là đường tròn bán kính \(\dfrac{2}{3}.3=2\)