Biết điều kiện cần và đủ của m để phương trình log 2 1 2 x - 2 2 + 4 m - 5 log 1 2 1 x - 2 - 8 m - 4 = 0 . Có nghiệm thuộc 5 4 ; 4 là m ∈ a ; b . Tính T=a+b
A. 10 3
B. 4
C. -4
D. - 10 3
Cho hai phương trình : \(X^2-2px+n=0\)(1) và \(X^2-2mx+n=0\)(2)
Tìm điều kiện cần và đủ để mỗi phương trình có 1 nghiệm nằm xen giữa hai nghiệm của phương trình còn lại.
Cho phương trình: \(^{x^2-2\left(m+1\right)x-\left(m+2\right)=0}\)
a) giải phương trình khi m=-2
b) tìm điều kiện của m để phương trình trên có 1 nghiệm x1=2
c) Tìm điều kiện của m để pt trên có nghiệm kép
Mong giúp đỡ
a) Thay m=-2 vào pt:
\(x^2-2.\left(-2+1\right).x-\left(-2+2\right)=0\\ \Leftrightarrow x^2+2x=0\\ \Leftrightarrow x.\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x+2=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-2\end{matrix}\right.\)
Với m= -2 => S= {-2;0}
b) Để phương trình trên có 1 nghiệm x1=2:
<=> 22 -2.(m+1).2-(m+2)=0
<=> 4-4m -4 -m-2=0
<=> -5m=2
<=>m=-2/5
c) ĐK của m để pt trên có nghiệm kép:
\(\Delta'=0\\ \Leftrightarrow\left(m+1\right)^2+1.\left(m+2\right)=0\\ \Leftrightarrow m^2+3m+3=0\)
Vô nghiệm.
Xét các phát biểu sau:
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là B A → = - 2 A C →
(2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là C B → = C A →
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là P Q → = 2 P M →
Trong các câu trên, thì:
A. Câu (1) và câu (3) là đúng
B. Câu (1) là sai.
C. Chỉ có câu (3) sai.
D. Không có câu nào sai.
Ta có
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là B A → = - 2 A C →
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là P Q → = 2 P M →
Phát biểu sai: (2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là
Do đó câu (1) và câu (3) là đúng.
Chọn A.
Để hệ phương trình x + y = S x . y = P có nghiệm, điều kiện cần và đủ là:
A. S 2 − P < 0
B. S 2 − P ≥ 0
C. S 2 − 4 P < 0
D. S 2 − P ≥ 0
- Ta có: x, y là nghiệm phương trình X 2 - S X + P = 0
- Hệ phương trình có nghiệm khi ∆ = S 2 - 4 P ≥ 0
Đáp án cần chọn là: D
Để hệ phương trình x + y = S x y = P có nghiệm, điều kiện cần và đủ là:
A. S 2 – P < 0
B. S 2 – P ≥ 0
C. S 2 – 4 P < 0
D. S 2 – 4 P ≥ 0
Để hệ phương trình x + y = S x . y = P có nghiệm, điều kiện cần và đủ là:
A. S 2 - P < 0
B. S 2 - P ≥ 0
C. S 2 - 4P < 0
D. S 2 - 4P ≥ 0
Đáp án D
Hệ phương trình đối xứng loại 1 với cách đặt 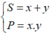 điều kiện
S
2
≥
4
P
⇔
S
2
-
4
P
≥
0
điều kiện
S
2
≥
4
P
⇔
S
2
-
4
P
≥
0
Xét các phát biểu sau:
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là B A → = - 2 A C →
(2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là C B → = C A →
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là P Q → = 2 P M →
Trong các câu trên, thì:
A. Câu (1) và câu (3) là đúng.
B. Câu (1) là sai.
C. Chỉ có câu (3) sai.
D. Không có câu nào sai.
Chọn A.
Ta có:
(1) Điều kiện cần và đủ để C là trung điểm của đoạn AB là ![]()
(3) Điều kiện cần và đủ để M là trung điểm của đoạn PQ là ![]()
Phát biểu sai: (2) Điều kiện cần và đủ để C là trung điểm của đoạn AB là ![]()
Do đó câu (1) và câu (3) là đúng.
cho phương trình \(\frac{x+2}{x-2}+\frac{m-x}{x+m+1}\)=0 với là ẩn , m là tham số. tìm điều kiện của m để phương trình vô nghiệm
ĐANG CẦN GẤP, CẢM ƠN!!!
ĐK: \(\hept{\begin{cases}x\ne2\\x\ne-m-1\end{cases}}\)
\(\frac{x+2}{x-2}+\frac{m-x}{x+m+1}=0\)(1)
=> ( x + 2 ) ( x + m + 1 ) + ( m - x ) ( x - 2 ) = 0
<=> (m + 3 ) x + 2 ( m + 1 ) + ( m + 2 ) x - 2m = 0
< => ( 2m + 5 ) x + 2 = 0 (2)
TH1: 2m + 5 = 0 <=> m = -5/2
Khi đó (2) trở thành: 0x + 2 = 0 => phương trình vô nghiệm với mọi x
=> m = -5/2 thỏa mãn
TH2: 2m + 5 \(\ne\)0 <=> m \(\ne\)-5/2
khi đó: (2) có nghiệm: \(x=-\frac{2}{2m+5}\)
( 1) vô nghiệm <=> (2) có nghiệm x = 2 hoặc x = -m -1
<=> \(\orbr{\begin{cases}-\frac{2}{2m+5}=-m-1\\-\frac{2}{2m+5}=2\end{cases}}\)
Giải: \(-\frac{2}{2m+5}=-m-1\)
<=> 2 = ( m + 1 ) ( 2m + 5 )
<=> 2m^2 +7m +3= 0
<=> m = -1/2 hoặc m = -3 (tm m khác -5/2)
Giải: \(-\frac{2}{2m+5}=2\)
<=> 2m + 5 = - 1 <=> m = - 3 (tm)
Vậy m = -5/2; m = -3; m = -1/2 thì phương trình vô nghiệm.
Mọi người giúp mình với ạ, mình cảm ơn rất nhiều
Câu 1: Cho bất phương trình x2 - 2mx + 8m - 7 > 0 (m là tham số thực). Điều kiện cần và đủ để bất phương trình nghiệm đùng với ∀x ∈ (-∞;0) là:
A. 1<m<7 B. 1≤m≤7 C. m≥\(\dfrac{7}{8}\) D. m≤\(\dfrac{7}{8}\)
Câu 2: Tập hợp tất cả các giá trị của tham số m để bất phương trình \(\sqrt{m-x}\) > x có tập nghiệm: A. (-∞;0) B. (1; +∞) C. (0; +∞) D. R
Câu 3: Biết rằng cos (x+70o) - cos(x+90o) - 2sin80ocos(x+80o) = asin(bx+co) là mệnh đề đúng với mọi góc lượng giác x (đơn vị: độ), a, b là các hằng số dương, c ∈[0;90]. Mệnh đề nào sau đây là đúng?
A. a+b+c=-3 B. a+b+c=1 C. a+b+c=3 D. a+b+c=-1
Câu 4: Trong mặt phẳng tọa độ Oxy cho đường tròn (C): (x-2)2 + (y+1)2 = 36 và điểm A(-2;2). Biết rằng d là đường thẳng đi qua A cắt đường tròn (C) tại hai điểm M, N sao cho dây cung MN có độ dài lớn nhất. Trong các điểm E(-1;1), F(\(\dfrac{-1}{2}\);4), G(-3;0), I(2;-1), điểm nào thuộc đường thẳng d?
A. Điểm F B. Điểm I C. Điểm E D. Điểm H
Câu 5: Tập hợp tất cả các tâm của họ đường tròn x2+y2-4(sinα)x + 4(cosα)y + 3 = 0 (α là tham số thực là):
A. Một đường thẳng B. Một đoạn thẳng C. Một đường tròn D. Một cung tròn