Tìm m để phương trình cos2x+2(m+1)sinx-2m-1=0 có đúng 3 nghiệm xϵ (0;π)
A. 0≤ m< 1.
B. -1< m< 1
C. 0< m≤1
D. 0< m< 1.
Tìm m để phương trình \(cos2x+\left(2m-3\right)sinx-m+1=0\) có đúng 7 nghiệm trên \(\left(-\dfrac{\pi}{6};3\pi\right)\)
1, cho phương trình \(sin2x-\left(2m+\sqrt{2}\right)\left(sinx+cosx\right)+2m\sqrt{2}+1=0\) tìm các giá trị m để phương trình có đúng 2 nghiệm \(x\in\left(0;\dfrac{5\Pi}{4}\right)\)
2,tìm tất cả các giá trị thực của tham số m để phương trình \(cos2x+\left(2m+1\right)sinx-m-1=0\) có đúng 2 nghiệm thuộc khoảng \(\left(\dfrac{\Pi}{2};\dfrac{3\Pi}{2}\right)\)
3, cho phương trình \(cos^2x-2mcosx+6m-9=0\) tìm các giá trị m để phương trình có nghiệm thuộc khoảng \(\left(-\dfrac{\Pi}{2};\dfrac{\Pi}{2}\right)\)
Tìm m để phương trình cos2x + 2(m+1)sĩn -2m-1=0 có đúng 3 nghiệm x ∈ 0 ; π
![]()
![]()
![]()
![]()
Tìm m để phương trình cos 2 x + 2 m + 1 sin x - 2 m - 1 = 0 có đúng 3 nghiệm x ∈ 0 ; π
![]()
![]()
![]()
![]()
Tìm các giá trị thực của tham số m để phương trình ( sin x - 1 ) . ( cos 2 x - cos x + m ) = 0 có đúng 5 nghiệm thuộc đoạn 0 , 2 π
A . 0 ≤ m ≤ 1 4
B . - 1 4 ≤ m ≤ 0
C . 0 ≤ m ≤ 1 4
D . - 1 4 < m < 0
Câu 1: Tích các nghiệm trên khoảng \(\left(\dfrac{\pi}{4};\dfrac{7\pi}{4}\right)\)của phương trình \(cos2x-3cosx+2=0\)
Câu 2: Tìm tất cả các giá trị thực của tham số m để phương trình \(2cos^23x+\left(3-2m\right)cos3x+m-2=0\) có đúng 3 nghiệm thuộc khoảng \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\).
Câu 3: Tính tổng T tất cả các nghiệm của phương trình \(2sin^2\dfrac{x}{4}-3cos\dfrac{x}{4}=0\) trên đoạn \(\left[0;8\pi\right]\).
Câu 4: Giá trị của m để phương trình \(cos2x-\left(2m+1\right)sinx-m-1=0\) có nghiệm trên khoảng \(\left(0;\pi\right)\) là \(m\in[a;b)\) thì a+b là?
Câu 5: Điều kiện cần và đủ để phương trình \(msinx-3cosx=5\) có nghiệm là \(m\in(-\infty;a]\cup[b;+\infty)\) với \(a,b\in Z\). Tính a+b.
Câu 6: Điều kiện để phương trình \(msinx-3cosx=5\) có nghiệm là?
Câu 7: Số nghiệm để phương trình \(sin2x+\sqrt{3}cos2x=\sqrt{3}\) trên khoảng \(\left(0;\dfrac{\pi}{2}\right)\) là?
Câu 8: Tập giá trị của hàm số \(y=\dfrac{sinx+2cosx+1}{sinx+cosx+2}\) là?
Câu 9: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn \(\left[-2018;2018\right]\) dể phương trình \(\left(m+1\right)sin^2-sin2x+cos2x=0\) có nghiệm?
Câu 10: Có bao nhiêu giá trị nguyên của tham số m để phương trình \(sin2x-cos2x+|sinx+cosx|-\sqrt{2cos^2x+m}-m=0\) có nghiệm thực?
1.
\(cos2x-3cosx+2=0\)
\(\Leftrightarrow2cos^2x-3cosx+1=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=k2\pi\\x=\pm\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(x=k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow\) không có nghiệm x thuộc đoạn
\(x=\pm\dfrac{\pi}{3}+k2\pi\in\left[\dfrac{\pi}{4};\dfrac{7\pi}{4}\right]\Rightarrow x_1=\dfrac{\pi}{3};x_2=\dfrac{5\pi}{3}\)
\(\Rightarrow P=x_1.x_2=\dfrac{5\pi^2}{9}\)
2.
\(pt\Leftrightarrow\left(cos3x-m+2\right)\left(2cos3x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos3x=\dfrac{1}{2}\left(1\right)\\cos3x=m-2\left(2\right)\end{matrix}\right.\)
\(\left(1\right)\Leftrightarrow x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\)
Ta có: \(x=\pm\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\pm\dfrac{\pi}{9}\)
Yêu cầu bài toán thỏa mãn khi \(\left(2\right)\) có nghiệm duy nhất thuộc \(\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}m-2=0\\m-2=1\\m-2=-1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}m=2\\m=3\\m=1\end{matrix}\right.\)
TH1: \(m=2\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{\pi}{6}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=\dfrac{\pi}{6}\left(tm\right)\)
\(\Rightarrow m=2\) thỏa mãn yêu cầu bài toán
TH2: \(m=3\)
\(\left(2\right)\Leftrightarrow cos3x=0\Leftrightarrow x=\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow x=0\left(tm\right)\)
\(\Rightarrow m=3\) thỏa mãn yêu cầu bài toán
TH3: \(m=1\)
\(\left(2\right)\Leftrightarrow cos3x=-1\Leftrightarrow x=\dfrac{\pi}{3}+\dfrac{k2\pi}{3}\in\left(-\dfrac{\pi}{6};\dfrac{\pi}{3}\right)\Rightarrow\left[{}\begin{matrix}x=\pm\dfrac{1}{3}\\x=-1\\x=-\dfrac{5}{3}\end{matrix}\right.\)
\(\Rightarrow m=2\) không thỏa mãn yêu cầu bài toán
Vậy \(m=2;m=3\)
3.
\(2sin^2\dfrac{x}{4}-3cos\dfrac{x}{4}=0\)
\(\Leftrightarrow2cos^2\dfrac{x}{4}+3cos\dfrac{x}{4}-2=0\)
\(\Leftrightarrow\left[{}\begin{matrix}cos\dfrac{x}{4}=\dfrac{1}{2}\\cos\dfrac{x}{4}=-2\left(l\right)\end{matrix}\right.\)
\(\Leftrightarrow x=\pm\dfrac{4\pi}{3}+k8\pi\in\left[0;8\pi\right]\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4\pi}{3}\\x=\dfrac{20\pi}{3}\end{matrix}\right.\)
\(\Rightarrow T=\dfrac{4\pi}{3}+\dfrac{20\pi}{3}=8\pi\)
Tìm m để phương trình 2sin2x – ( 2m+1) . sinx+ m = 0 có nghiệm x ∈ - π 2 ; 0
A. – 1< m < 0
B. 1< m< 2
C. – 1< m< 0
D. 0< m< 1
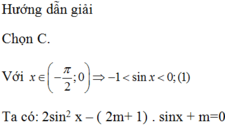
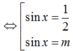
Phương trình sinx = 1/2 không có nghiệm x ∈ - π 2 ; 0
Nên để phương trình đã cho có nghiệm x ∈ - π 2 ; 0 khi và chỉ khi phương trình sinx = m có nghiệm trên khoảng đó. Kết hợp với (*) suy ra -1< m< 0
Tìm m để phương trình 2sin2x – (2m + 1)sinx + m = 0 có nghiệm x ∈ ( - π 2 ; 0).
A. -1 < m
B. 1 < m
C. -1 < m < 0
D. 0 < m < 1
Bài 1: Tìm m để các phương trình sau có nghiệm
a) \((m+2)sinx+mcosx=2\)
b) \(msinx+(m-1)cosx=2m+1\)
c) \((m+2)sin2x+mcos^2x=m-2+msin^2x\)
Bài 2: Tìm m để các phương trình sau vô nghiệm
a) \((2m-1)sinx+(m-1)cosx=m-3\)
b) \(2sinx+cosx=m(sinx-2cosx+3)\)
1.
a, Phương trình có nghiệm khi:
\(\left(m+2\right)^2+m^2\ge4\)
\(\Leftrightarrow m^2+4m+4+m^2\ge4\)
\(\Leftrightarrow2m^2+4m\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge0\\m\le-2\end{matrix}\right.\)
b, Phương trình có nghiệm khi:
\(m^2+\left(m-1\right)^2\ge\left(2m+1\right)^2\)
\(\Leftrightarrow2m^2+6m\le0\)
\(\Leftrightarrow-3\le m\le0\)
2.
a, Phương trình vô nghiệm khi:
\(\left(2m-1\right)^2+\left(m-1\right)^2< \left(m-3\right)^2\)
\(\Leftrightarrow4m^2-4m+1+m^2-2m+1< m^2-6m+9\)
\(\Leftrightarrow4m^2-7< 0\)
\(\Leftrightarrow-\dfrac{\sqrt{7}}{2}< m< \dfrac{\sqrt{7}}{2}\)
b, \(2sinx+cosx=m\left(sinx-2cosx+3\right)\)
\(\Leftrightarrow\left(m-2\right)sinx-\left(2m+1\right)cosx=-3m\)
Phương trình vô nghiệm khi:
\(\left(m-2\right)^2+\left(2m+1\right)^2< 9m^2\)
\(\Leftrightarrow m^2-4m+4+4m^2+4m+1< 9m^2\)
\(\Leftrightarrow m^2-1>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
1.
c, \(\left(m+2\right)sin2x+mcos^2x=m-2+msin^2x\)
\(\Leftrightarrow\left(m+2\right)sin2x+m\left(cos^2x-sin^2x\right)=m-2\)
\(\Leftrightarrow\left(m+2\right)sin2x+mcos2x=m-2\)
Phương trình vô nghiệm khi:
\(\left(m+2\right)^2+m^2< \left(m-2\right)^2\)
\(\Leftrightarrow m^2+4m+4+m^2< m^2-4m+4\)
\(\Leftrightarrow m^2+8m< 0\)
\(\Leftrightarrow-8\le m\le0\)