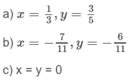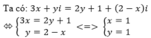Tìm các số thực x, y sao cho: 2x+y-1=(x+2y-5)i

Những câu hỏi liên quan
Tìm các số thực x, y sao cho :
a) \(3x+yi=2y+1+\left(2-x\right)i\)
b) \(2x+y-1=\left(x+2y-5\right)i\)
a)3x+yi=(2y+1)(2−x)i⇔{3x=2y+1y=2−x⇔{x=1y=13x+yi=(2y+1)(2−x)i⇔{3x=2y+1y=2−x⇔{x=1y=1
b)2x+y−1=(x+2y−5)i⇔{2x+y−1=0x+2y−5=0⇔{x=−1y=3
Đúng 0
Bình luận (0)
Tìm các số thực x và y, biết:
(2x + y) + (2y - x)i = (x - 2y + 3) + (y + 2x + 1)i
(2x + y) + (2y - x)i = (x - 2y + 3) + (y + 2x + 1)i
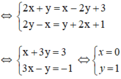
Đúng 0
Bình luận (0)
Tìm các số thực x, y thỏa mãn:
a) 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
b) 4x + 3 + (3y – 2)i = y +1 + (x – 3)i
c) x + 2y + (2x – y)i = 2x + y + (x + 2y)i
Tìm các số thực x, y thỏa mãn: x + 2y + (2x – y)i = 2x + y + (x + 2y)i
Tìm các số thực x, y sao cho: 3x+yi=2y+1+(2-x)i
Tìm các số thực x,y thỏa mãn
2
x
-
1
+
(
1
-
2
y
)
i
2
-
x
+
(
3
y
+
2
)
i
A.
x
1
;
y
3
5
B.
x
3
;
y
3...
Đọc tiếp
Tìm các số thực x,y thỏa mãn 2 x - 1 + ( 1 - 2 y ) i = 2 - x + ( 3 y + 2 ) i
A. x = 1 ; y = 3 5
B. x = 3 ; y = 3 5
C. x = 3 ; y = - 1 5
D. x = 1 ; y = - 1 5
Tìm các số thực x, y thỏa mãn: 2x + 1 + (1 – 2y)i = 2 – x + (3y – 2)i
Tìm các số thực x và y, biết :
a) \(\left(3x-2\right)+\left(2y+1\right)i=\left(x+1\right)-\left(y-5\right)i\)
b) \(\left(1-2x\right)-i\sqrt{3}=\sqrt{5}+\left(1-3y\right)i\)
c) \(\left(2x+y\right)+\left(2y-x\right)i=\left(x-2y+3\right)+\left(y+2x+1\right)i\)
Từ định nghĩa bằng nhau của hai số phức, ta có:
a) ⇔
;
b) ⇔
;
c) ⇔
⇔
.
Đúng 0
Bình luận (0)
cho x,y là các số thực dương thỏa mãn: 1≤x≤2, 1≤y≤2. Tìm giá trị nhỏ nhất.
P=\(\dfrac{x+2y}{x^2+3y+5}+\dfrac{y+2x}{y^2+3x+5}+\dfrac{1}{4\left(x+y-1\right)}\)
Do \(1\le x\le2\Rightarrow\left(x-1\right)\left(x-2\right)\le0\)
\(\Leftrightarrow x^2+2\le3x\)
Hoàn toàn tương tự ta có \(y^2+2\le3y\)
Do đó: \(P\ge\dfrac{x+2y}{3x+3y+3}+\dfrac{2x+y}{3x+3y+3}+\dfrac{1}{4\left(x+y-1\right)}\)
\(P\ge\dfrac{x+y}{x+y+1}+\dfrac{1}{4\left(x+y-1\right)}\)
Đặt \(a=x+y-1\Rightarrow1\le a\le3\)
\(\Rightarrow P\ge f\left(a\right)=\dfrac{a+1}{a+2}+\dfrac{1}{4a}\)
\(f'\left(a\right)=\dfrac{3a^2-4a-4}{4a^2\left(a+2\right)^2}=\dfrac{\left(a-2\right)\left(3a+2\right)}{4a^2\left(a+2\right)^2}=0\Rightarrow a=2\)
\(f\left(1\right)=\dfrac{11}{12}\) ; \(f\left(2\right)=\dfrac{7}{8}\) ; \(f\left(3\right)=\dfrac{53}{60}\)
\(\Rightarrow f\left(a\right)\ge\dfrac{7}{8}\Rightarrow P_{min}=\dfrac{7}{8}\) khi \(\left(x;y\right)=\left(1;2\right);\left(2;1\right)\)
Đúng 0
Bình luận (0)