Cho mẫu số liệu thống kê {6;4;4;1;9;10;7} . Số liệu trung vị của mẫu số liệu thống kê trên là:
A. 1
B. 6
C. 4
D. 10
Cho mẫu số liệu thống kê: {5;2;1;6;7;5;4;5;9}. Mốt M 0 của mẫu số liệu trên bằng bao nhiêu?
A. 3
B. 5
C. 9
D. 7
Đáp án B.
Giá trị 5 xuất hiện nhiều lần nhất trong mẫu số liệu (3 lần)
⇒ M 0 = 5
Thống kê số huy chương bốn quốc gia dẫn đầu SEA Games 31 được cho trong bảng số liệu sau:
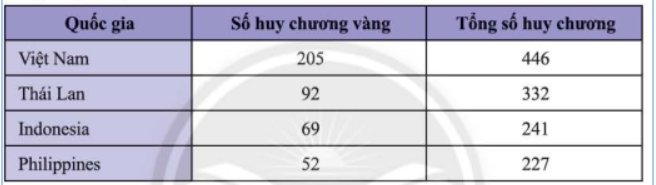
Hãy chuyển dữ liệu đã cho vào bảng thống kê theo mẫu dưới đây và vào biểu đồ cột kép tương ứng.

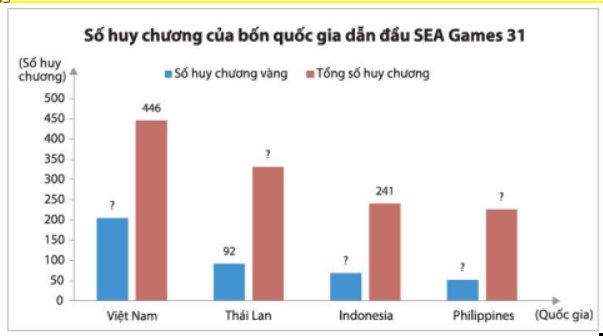
Điền số vào bảng: 446 92 69 227
Biểu đồ; 205 322 69 52 227
Cho dãy số liệu thống kê: 5; 6; 7; 8; 9. Phương sai của dãy số liệu thống kê trên là:
A. 10
B. 7
C. 6
D.2
Đáp án D.
+ Trung bình cộng của dãy là x ¯ = 7
+ Phương sai của dãy số liệu thống kê là:
S 2 = 1 5 - 7 2 + 1 . 6 - 7 2 + 1 . 7 - 7 2 + 1 . 8 - 7 2 + 1 . 5 5 S 2 = 10 5 = 2
cho bảng thống kê điểm lớp 10A1
| điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| số hs | 2 | 3 | 7 | 18 | 3 | 2 | 4 | 1 |
tìm độ lệch chuẩn của mẫu số liệu trên
Cho dãy số liệu thống kê : 1, 2, 3, 4, 5, 6, 7
Hỏi phương sai của các số liệu thống kê đã cho là bao nhiêu ?
là 4 vì \(S^2=\dfrac{3^2+2^2+1^2+0^2+1^2+2^2+3^2}{7}=4\)
Biểu đồ đoạn thẳng ở Hình 6 cho biết lượng khách du lịch quốc tế đến Việt Nam trong một số năm (từ 1990 đến 2019).
a) Viết mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên.
b) Viết mẫu số liệu theo thứ tự tăng dần. Tìm số trung bình cộng, trung vị và tứ phân vị của mẫu số liệu đó.
c) Tìm khoảng biến thiên và khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
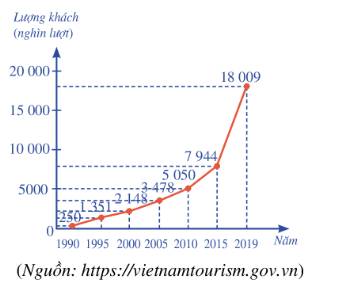
a) Mẫu số liệu thống kê số lượt khách du lịch Lượng khách quốc tế đến Việt Nam nhận được từ biểu đồ bên là:
250 1351 2148 3478 5050 7944 18009
b) Sắp xếp mẫu số liệu theo thứ tự không giảm ta được: 250 1351 2148 3478 5050 7944 18009
Số trung bình cộng của mẫu số liệu trên là:
\(\overline x = \frac{{250{\rm{ + }}1351{\rm{ + }}2148{\rm{ + }}3478{\rm{ + }}5050{\rm{ + }}7944{\rm{ + }}18009}}{7} = \frac{{38230}}{7}\)
Trung vị của mẫu số liệu trên là: Do mẫu số liệu trên có 7 số liệu ( lẻ ) nên trung vị \({Q_2} = 3478\)
Tứ phân vị của mẫu số liệu trên là:
- Trung vị của dãy 250 1351 2148 là: \({Q_1} = 1351\)
- Trung vị của dãy 5050 7944 18009 là: \({Q_3} = 7944\)
- Vậy tứ phân vị của mẫu số liệu là: \({Q_1} = 1351\), \({Q_2} = 3478\), \({Q_3} = 7944\)
c) Khoảng biến thiên của mẫu số liệu trên là: \(R = {x_{\max }} - {x_{\min }} = 18009 - 250 = 17759\)
Khoảng tứ phân vị của mẫu số liệu trên là: \({\Delta _Q} = {Q_3} - {Q_1} = 7944 - 1351 = 6593\)
d) Phương sai của mẫu số liệu trên là:
\({s^2} = \frac{{\left[ {{{\left( {250 - \overline x } \right)}^2} + {{\left( {351 - \overline x } \right)}^2} + ... + {{\left( {18009 - \overline x } \right)}^2}} \right]}}{7} \approx 31820198,82\)
Độ lệch chuẩn của mẫu số liệu trên là: \(s = \sqrt {{s^2}} \approx 5640,93\)
Số liệu thống kê điểm kiểm tra môn Toán của học sinh lớp 10A được cho trong bảng sau:
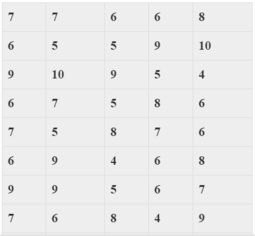

Đơn vị điều tra và kích thước mẫu của bảng số liệu trên là:
A. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44
B. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45
C. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45
D. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44
Chọn A.
Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A
Liệt kê số điểm của 44 học sinh lớp 10A nên kích thước mẫu của số liệu là 44.
Bảng 6 thống kê số áo sơ mi nam bán được của một cửa hàng trong một tháng.
Cỡ áo | 36 | 37 | 38 | 39 | 40 | 41 | 42 |
Tần số (Số áo bán được) | 28 | 30 | 31 | 47 | 45 | 39 | 32 |
Bảng 6 Mốt của mẫu số liệu trên là bao nhiêu?
A. 42.
B. 47.
C. 32.
D. 39.
Dựa vào bảng tần số, ta thấy tần số lớn nhất là 47 ứng với cỡ áo 39. Vậy mốt của mẫu số liệu là 39.
Biểu đồ đoạn thẳng ở Hình 4 biểu diễn giá vàng bán ra trong bảy ngày đầu tiên của tháng 6 năm 2021.
a) Viết mẫu số liệu thống kê giá vàng bán ra nhận được từ biểu đồ ở Hình 4.
b) Tìm khoảng biến thiên của mẫu số liệu đó.
c) Tìm khoảng tứ phân vị của mẫu số liệu đó.
d) Tính phương sai và độ lệch chuẩn của mẫu số liệu đó.
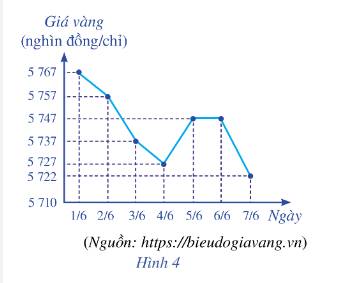
a) Dựa vào biểu đồ, ta có mẫu số liệu là:
5767 5757 5737 5727 5747 5747 5722
b) Khoảng biến thiên của mẫu số liệu đó là: \(R = {x_{\max }} - {x_{\min }} = 5767 - 5722 = 45\)
c) +) Sắp xếp mẫu số liệu theo thứ tự không giảm, ta có:
5722 5727 5737 5747 5747 5757 5767
+) Các tứ phân vị của mẫu số liệu là:
Trung vị của mẫu số liệu: \({Q_2}\) = 5747.
Trung vị của dãy 5722 5727 5737 là: \({Q_1}\) = 5727.
Trung vị của dãy 5747 5757 5767 là: \({Q_3}\) = 5757.
+) Khoảng tứ phân vị của mẫu số liệu là: \({\Delta _Q} ={Q_3} - {Q_1}\) = 5757- 5727= 30.
d) +) Giá vàng trung bình trong 7 ngày đầu tiên của tháng 6 năm 2021 là: \(\overline x = \frac{{5722{\rm{ + }}5727{\rm{ + }}5737{\rm{ + }}5747{\rm{ + }}5747{\rm{ + }}5757{\rm{ + }}5767}}{7} = 5743,43\) ( nghìn đồng/ chỉ)
+) Phương sai của mẫu số liệu là: \({s^2} = \frac{{\left[ {{{\left( {5722 - \overline x } \right)}^2} + {{\left( {5727 - \overline x } \right)}^2} + ... + {{\left( {5767 - \overline x } \right)}^2}} \right]}}{7} \approx 219,39\)
+) Độ lệch chuẩn của của mẫu số liệu là: \(s = \sqrt {{s^2}} = \sqrt {219,39} \approx 14,81\)( nghìn đồng/ chỉ)