Giá trị của biểu thức A = sin4x + cos4x - ¼cos 4x là:
A. 2
B. 1
C. 0,75
D. 0,25
Những câu hỏi liên quan
Giá trị của biểu thức A = sin4x + cos4x
Biểu thức A = 3(sin4x + cos4x) - 2 (sin6x + cos6x) có giá trị bằng:
A. 1
B. 2
C. -1
D. 0
Chọn A.
Ta có:
+ sin4x + cos4x = (sin2x + cos2x)2 - 2sin2x.cos2x = 1 - 2sin2x.cos2x.
+ sin4x + cos4x = 1 - 3sin2x.cos2x.
Do đó
A = 3(1 - 2sin2x.cos2x) - 2(1 - 3sin2x.cos2x) = 1.
Đúng 0
Bình luận (0)
Giá trị lớn nhất của biểu thức P = sin 4 x + cos 4 x + sin x . cos x là:
A. 2
B. 1
C. 9 8
D. 2
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào x.A 2(
sin
4
x
+
cos
4
x
+
sin
2
x
.
cos
2
x
)
2
- (
sin
8
x
+
cos
8
x
)
Đọc tiếp
Chứng minh rằng giá trị của biểu thức sau không phụ thuộc vào x.
A = 2( sin 4 x + cos 4 x + sin 2 x . cos 2 x ) 2 - ( sin 8 x + cos 8 x )
Ta có:
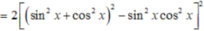
Vậy giá trị của biểu thức 
không phụ thuộc vào x.
Đúng 0
Bình luận (0)
Biểu thức B
sin
4
x
+
cos
4
x
-
1
tan
2
x
+
c
o
t
2
x
+...
Đọc tiếp
Biểu thức B= sin 4 x + cos 4 x - 1 tan 2 x + c o t 2 x + 2 có giá trị không đổi bằng:
A. 2
B. 1
C. -2
D. -1
Biểu thức
B
sin
4
x
+
cos
4
x
−
1
tan
2
x
+
cot...
Đọc tiếp
Biểu thức B = sin 4 x + cos 4 x − 1 tan 2 x + cot 2 x + 2 có giá trị không đổi bằng:
A. 2
B. 1
C. -2
D. -1
Chứng minh các đẳng thức:
\(cos^3xsinx-sin^3xcosx=\dfrac{1}{4}sin4x\)
\(sin^4x+cos^4x=\dfrac{1}{4}\left(3+cos4x\right)\)
\(cos^3xsinx-sin^3xcosx=sinx.cosx\left(cos^2x-sin^2x\right)=\dfrac{1}{2}sin2x.cos2x=\dfrac{1}{4}sin4x\)
\(sin^4x+cos^4x=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x=1-\dfrac{1}{2}\left(2sinx.cosx\right)^2=1-\dfrac{1}{2}sin^22x\)
\(=1-\dfrac{1}{2}\left(\dfrac{1}{2}-\dfrac{1}{2}cos4x\right)=\dfrac{3}{4}+\dfrac{1}{4}cos4x=\dfrac{1}{4}\left(3+cos4x\right)\)
Đúng 2
Bình luận (0)
Rút gọn biểu thức C 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x) có giá trị không đổi và bằng A. 2 B. 4 C. 1 D. 0
Đọc tiếp
Rút gọn biểu thức C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x) có giá trị không đổi và bằng
A. 2
B. 4
C. 1
D. 0
Chọn C.
Ta có: C = 2( sin4x + cos4x + sin2x.cos2x) 2 - ( sin8x + cos8x)
= 2 [ (sin2x + cos2x) 2 - sin2x.cos2x]2 - [ (sin4x + cos4x)2 - 2sin4x.cos4x]
= 2[ 1 - sin2x.cos2x]2 - [ (sin2x+ cos2x) 2 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2[ 1- sin2x.cos2x]2 - [ 1 - 2sin2x.cos2x]2 + 2sin4x.cos4x
= 2( 1 - 2sin2xcos2x+ sin4x.cos4x) –( 1- 4sin2xcos2x+ 4sin4xcos4x) + 2sin4x.cos4x
= 1.
Đúng 1
Bình luận (0)
1. Rút gọn biểu thức Pcos^4x-sin^4xA.Pcos2x B.Pdfrac{3}{4}+dfrac{1}{4}cos4x C.Pdfrac{1}{4}+dfrac{3}{4}cos4x D.Pdfrac{3}{4}-dfrac{1}{4}cos4x2.Đơn giản biểu thức Dsinleft(dfrac{5pi}{2}-alpharight)+cosleft(13pi+alpharight)-3sinleft(alpha-5piright)A.3sina-2cosa B.3sina C.-3sina D.2cosa+3sinaTrắc nghiệm nhưng mong mn trình bày bài làm giúp em để tham khảo với ạ. Em cảm ơn
Đọc tiếp
1. Rút gọn biểu thức \(P=cos^4x-sin^4x\)
\(A.P=cos2x\) \(B.P=\dfrac{3}{4}+\dfrac{1}{4}cos4x\) \(C.P=\dfrac{1}{4}+\dfrac{3}{4}cos4x\) \(D.P=\dfrac{3}{4}-\dfrac{1}{4}cos4x\)
2.Đơn giản biểu thức \(D=sin\left(\dfrac{5\pi}{2}-\alpha\right)+cos\left(13\pi+\alpha\right)-3sin\left(\alpha-5\pi\right)\)
\(A.3sina-2cosa\) \(B.3sina\) \(C.-3sina\) \(D.2cosa+3sina\)
Trắc nghiệm nhưng mong mn trình bày bài làm giúp em để tham khảo với ạ. Em cảm ơn
1.Ý A
\(P=cos^4x-sin^4x=\left(cos^2x-sin^2x\right)\left(cos^2x+sin^2x\right)=cos2x\)
2. Ý B
\(D=sin\left(\dfrac{5\pi}{2}-\alpha\right)+cos\left(13\pi+\alpha\right)-3sin\left(\alpha-5\pi\right)\)
\(=sin\left(2\pi+\dfrac{\pi}{2}-\alpha\right)+cos\left(\pi+\alpha+12\pi\right)-3sin\left(\alpha+\pi-6\pi\right)\)
\(=sin\left(\dfrac{\pi}{2}-\alpha\right)+cos\left(\pi+\alpha\right)-3sin\left(\alpha+\pi\right)\)
\(=cos\alpha-cos\alpha+3sin\alpha=3sin\alpha\)
Đúng 1
Bình luận (0)