Tam giác ABC có A ^ = 100 o , B ^ - C ^ = 40 o . Số đo góc B và góc C lần lượt là:
A. B ^ = 60 ° , C ^ = 20 °
B. B ^ = 20 ° , C ^ = 60 °
C. B ^ = 70 ° , C ^ = 20 °
D. B ^ = 80 ° , C ^ = 30 °
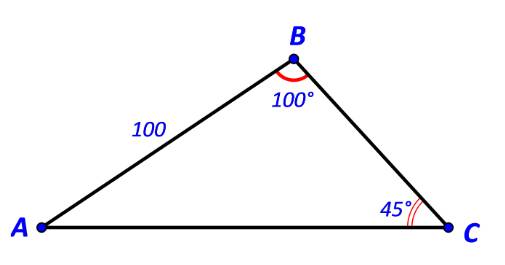
Cho tam giác ABC có \(AB = 100,\widehat B = {100^o},\widehat C = {45^o}.\) Tính:
a) Độ dài các cạnh AC, BC
b) Diện tích tam giác ABC.
a)
Ta có: \(\widehat A = {180^o} - (\widehat B + \widehat C)\) \( \Rightarrow \widehat A = {180^o} - ({100^o} + {45^o}) = {35^o}\)
Áp dụng định lí sin trong tam giác ABC ta có:
\(\frac{{AB}}{{\sin C}} = \frac{{AC}}{{\sin B}} = \frac{{BC}}{{\sin A}}\)
\( \Rightarrow \left\{ \begin{array}{l}AC = \sin B.\frac{{AB}}{{\sin C}}\\BC = \sin A.\frac{{AB}}{{\sin C}}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}AC = \sin {100^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 139,3\\BC = \sin {35^o}.\frac{{100}}{{\sin {{45}^o}}} \approx 81,1\end{array} \right.\)
b)
Diện tích tam giác ABC là: \(S = \frac{1}{2}.BC.AC.\sin C = \frac{1}{2}.81,1.139,3.\sin {45^o} \approx 3994,2.\)
a, Cho tam giác ABC biết \(\widehat{A}=100^o,\widehat{B}-\widehat{C}=50^o.Tính\widehat{B},\widehat{C}\)
b, Tam giác ABC có\(\widehat{B}=80^o,3\widehat{A}=2\widehat{C}.Tính\widehat{A},\widehat{C}\)
a)
=> Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}\) = 180o
100o + \(\widehat{B}+\widehat{C}\) = 180o
\(\widehat{B}+\widehat{C}\) = 180o - 100o
\(\widehat{B}+\widehat{C}\) = 80o
Góc B = (80o+50o):2 = 65o
=> \(\widehat{C}\) = 65o - 50o = 15o
Vậy \(\widehat{B}\) = 65o ; \(\widehat{C}\) = 15o
b)
Ta có : \(\widehat{3A}+\widehat{B}+\widehat{2C}\) = 180o
\(\widehat{3A}+\widehat{2C}\) = 180o - 80o
\(\widehat{3A}+\widehat{2C}\) = 100o
=> \(\widehat{A}\) = 100o:(3+2).3 = 60o
\(\widehat{C}\) = 100o - 60o = 40o
Vậy \(\widehat{A}\) = 60o ; \(\widehat{C}\) = 40o
Tam giác ABC cân tại A có \(\widehat{A}\) \(=40^o\) thì góc ngoài tại đỉnh C bằng:
A. \(40^o\) B. \(90^o\) C. \(100^o\) D. \(110^o\)
Cho tam giác ABC có góc A= 100 góc B=50 độ. Tia p giác trong của tam giác ABC tại b cắt tia p giác ngoài tại C ở điểm O. Tính góc BOC và góc AOB
Cho tam giác ABC có \(\widehat A = \)\({100^0}\),\(\widehat B\)\( = {40^o}\).
a) Tìm cạnh lớn nhất của tam giác ABC.
b) Tam giác ABC là tam giác gì? Vì sao?
a) Do \(\widehat{A}=100^0>90^0\) nên là góc tù, do đó, \(\widehat{A}\) là góc lớn nhất trong tam giác ABC.
\( \Rightarrow \) BC là cạnh lớn nhất của tam giác ABC (do BC đối diện với góc A trong tam giác ABC)
b)
Theo định lí tổng 3 góc trong tam giác ABC, ta có:
\( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat C = {180^o} - {100^o} - {40^o} = {40^o}\)
\( \Rightarrow\widehat C = \widehat B = {40^o}\)
\( \Rightarrow \) ABC là tam giác cân tại A.
cho tam giác ABC có goc A=100o , góc B - C = 50o.Tính góc B,C
^B+^C=1800-1000=800
=> ^C=(800-500)/2=150
^B=150+500=650
ĐS: ^B=650; ^C=150.
Ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) và \(\widehat{A}=100^o\) ; \(\widehat{B}-\widehat{C}=50^o\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}-\widehat{A}=180^o-100^o\)
\(\Rightarrow\widehat{B}+\widehat{C}=80^0\) mà \(\widehat{B}-\widehat{C}=50^0\)
\(\Rightarrow\widehat{B}=\left(\widehat{B}+\widehat{C}-\left(\widehat{B}-\widehat{C}\right)\right)\left(80^o+50^0\right):2=65^0\)
\(\Rightarrow\widehat{C}=\widehat{B}-50^0=65^0-50^0=15^0\)
tam giác ABC có \(\widehat{A}\)+ \(\widehat{B}\)+ \(\widehat{C}\)= \(180^0\)
\(100^0\)+ \(\widehat{B}\)+ \(\widehat{C}\)= \(180^0\)
\(\Rightarrow\)\(\widehat{B}\)+ \(\widehat{C}\) = \(80^0\) (1)
mà \(\widehat{B}\)- \(\widehat{C}\)= \(50^0\)\(\Rightarrow\)\(\widehat{B}\)= \(50^0\)+ \(\widehat{C}\) (2)
Thay (2) vào (1) ta được:
\(50^0\)+ \(\widehat{C}\)+ \(\widehat{C}\)= \(180^0\)
\(50^0\)+ 2\(\widehat{C}\) = \(180^0\)
2\(\widehat{C}\) = \(130^0\)
\(\widehat{C}\) = \(65^0\)
\(\Rightarrow\) \(\widehat{B}\)= \(50^0\)+ \(65^0\)= \(115^0\)
Vậy...
Cho tam giác ABC cân tại A có góc A bằng 100o , BC=a, AC=b. Về phía ngoài tam giác ABC vẽ tam giác ABD cân ở D có góc ADB = 140o. Tính chu vi tam giác ABD theo a và b.
Cho tam giác ABC có góc A=100o ; Góc B-C=20o . Tính góc B và góc C
trong tam giác ta có
A+B+C=180
=> B+C=180-A=180-100=80
theo đề ta có hệ pt: \(\begin{cases}B+C=80\\B-C=20\end{cases}\)
<=> \(\begin{cases}B=50\\C=30\end{cases}\)
vậy B=50 dộ
C=30 độ
Xét \(\Delta ABC\) có:
\(\widehat {A} + \widehat {B} + \widehat {C} = 180^O\)(Định lí tổng 3 góc của 1 tam giác)
\(100^O + \widehat {B} + \widehat {C} = 180^O\)(\(\widehat {A} = 100^O (gt)\))
\(\widehat {B} + \widehat {C} = 180^O - 100^O\)
\(\widehat {B} + \widehat {C} = 80^O\) (1)
Mà \(\widehat {B} - \widehat {C} = 20^O\) (2)
Từ (1)(2), cộng vế với vế ta có:
\(2\widehat {B} = 100^O\)
\(\Rightarrow\)\(\widehat {B} = 100^O:2=50^O\)
\(\Rightarrow\)\(\widehat {C} = 50^O - 20^O = 30^O\)
Vậy \(\widehat {B} = 50^O; \widehat {C} = 30^O\)
Cho tam giác ABC có góc A=100° , góc B=50°. Tia phân giác trong tại đỉnh B cắt tia phân giác ngoài tại đỉnh C của tam giác ABC tại O. Tính số đo góc BOC và góc AOB
Help me
5b
Cho tam giac ABC, D la 1 điểm trên cạnh BC, O là đểm nằm bên trong tam giác
a) so sánh góc ADC va ABC?
b) so sánh góc BOC VA BAC ?
10
cho tam giác ABC (B < C) có A +2B +100. Tính số đo C-B
7b
cho tam giác ABC có góc B tù. Chướng minh rằng các góc A và C nhọn.
5b
a)\(\widehat{ADC}>\widehat{ABC}\)
b)\(\widehat{BOC}>\widehat{BAC}\)
7b
Theo định lí tổng ba góc trong 1 tam giác ta có
\(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)
Mà \(\widehat{B}\)là góc tù => \(\widehat{B}>90^o\)
Tổng 3 góc trg 1 tam giác = 180 độ => A + C = 180 - B
(Giả sử góc B = 80 độ và A = C thì ta có A + C = 180 - 80 = 90 => A = C = 100/2 = 50 độ)
Từ trên suy ra góc A và góc C là 2 góc nhọn
bài 7b
B>90
mà sao B=80
xin lỗi mik sửa
Giả sử góc B = 100 độ và A = C thì ta có A + C = 180 - B = 180 - 100 = 80 => A = C = 80/2 = 40
#Học tốt!!!