Cho hình vẽ sau biết AB // DE. Tính A C D ^
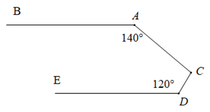
A. 100 °
B. 140 °
C. 120 °
D. 140 °
Những câu hỏi liên quan
cho hình vẽ . chứng minh AB song song với CD B A E C D 100 độ 120 độ 140 độ
Cho hình vẽ biết DE //Ax,xAB=30°,DBC=60°,Bcy=120°
A,Tính ABE
B,CMR:cy//Ax
C,AB vuông góc với BC
Cho hình vẽ sau , biết ABC+BCD+CDE360. Chứng tỏ AB//DE. A B C D E
Đọc tiếp
Cho hình vẽ sau , biết ABC+BCD+CDE=360. Chứng tỏ AB//DE.
Kẻ Cz // AB
⇒ˆABC+ˆBCz=180°⇒ABC^+BCz^=180°(2 góc trrong cùng phía bù nhau)
Ta có: ˆABC+ˆBCD+ˆCDE=360°ABC^+BCD^+CDE^=360°
=ˆABC+ˆBCz+ˆzCD+ˆCDE=360°=ABC^+BCz^+zCD^+CDE^=360°
⇒180°+ˆzCD+ˆCDE=360°⇒180°+zCD^+CDE^=360°
⇒ˆzCD+ˆCDE=360°−180°=180°⇒zCD^+CDE^=360°-180°=180° mà 2 góc này nằm ở vị trí trong cùng phía
=> DE // Cz mà Cz // AB
=> AB // DE (đpcm)
Đúng 4
Bình luận (0)
cho hình vẽ, biết m//n. tính B, biết A125,C140. A M B C N 125 140
Đọc tiếp
cho hình vẽ, biết m//n. tính B, biết A=125,C=140.
Cho ABC có góc A 120 , đường phân giác AD ( D thuộc cạnh BC). Vẽ DE vuông góc với AB, vẽ DF vuông góc với AC.
a. Chứng minh: DE = DF và EDF 60
b. Lấy K nằm giữa E và B, I nằm giữa F và C sao cho EK = FI. CMR: DK = DI
c. Từ C kẻ đường thẳng song song với AD cắt AB tại M. Tính các góc của AMC
d. Tính DF biết AD = 4cm
1.Trong hình vẽ bên, biết AB//CD,BAE=140 và AEC=120
a) Tính số đo góc ECD.
b) CM: EAB+ECD+AEC=360
Cho hình vẽ biết rằng cd// ey, góc bax=140, góc bey=130, abd=40
a, tính cbe
b, chứng minh ax// ey
c, chứng minh ab vuông góc be
Bài 1: Cho hình vẽ, biết nperp AB tại B, widehat{F_1}120^o.a) Chứng tỏ m//n.b) Tính widehat{E_1}.c) Chứng tỏ mperp AB. Vì sao? E 1 ? F A m n B 120 độ 1
Đọc tiếp
Bài 1: Cho hình vẽ, biết \(n\perp AB\) tại B, \(\widehat{F_1}\)=\(120^o\).
a) Chứng tỏ m//n.
b) Tính \(\widehat{E_1}\).
c) Chứng tỏ \(m\perp AB\). Vì sao?
chứng tỏ AB//EF trong mỗi hình sauhình a A B C D E F 120 độ 60 độ 40 độ 140 độ hình b C D E F A B 30 độ 30 độ 40 độ 40 độ
Đọc tiếp
chứng tỏ AB//EF trong mỗi hình sau
hình a
hình b
hình a, ta thấy
\(\angle\left(A\right)+\angle\left(DCA\right)=120+60=180^0\)
mà 2 góc này ở vị trí trong cùng phía
\(=>AB//CD\left(1\right)\)
có \(\angle\left(DCE\right)+\angle\left(E\right)=40+140=180^O\)
mà 2 góc này ở vị trí trong cùng phía
\(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
hình b,
\(=\angle\left(BAD\right)=\angle\left(ADC\right)=30^0\)
mà 2 góc này ở vị trí so le trong \(=>AB//CD\left(1\right)\)
có \(\angle\left(CDE\right)=\angle\left(DEF\right)=40^o\)
mà 2 góc này ở vị trí so le trong \(=>CD//EF\left(2\right)\)
(1)(2)\(=>AB//EF\)
Đúng 2
Bình luận (0)
cho hình thang ABCD (AB//CD). tính số đo góc B và góc D biết góc A = 140 độ, góc c = 45 độ
Vì AB//CD (gt) ⇒ A+D=1800 ➩1400 + D = 180o ⇒ D = 40o
⇒B + C =180o ⇒ B + 45o = 180o ⇒ B + 45o = 180o ⇒ B=135o
Đúng 0
Bình luận (0)
Ta có: AB//CD(gt)
nên \(\widehat{A}+\widehat{D}=180^0\)
hay \(\widehat{D}=40^0\)
Ta có: AB//CD(gt)
nên \(\widehat{B}+\widehat{C}=180^0\)
hay \(\widehat{B}=135^0\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời