Cho hình vẽ , có B 1 ^ = 42 o , D 1 ^ = 53 o và AB//CD. Số đo của góc x O y ^
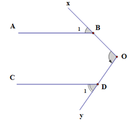
A. 100 °
B. 90 °
C. 105 °
D. 95 °
Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.
a) Cho biết \(\widehat {{A_1}}\)\( = {42^o}\). Tính số đo của \(\widehat {{M_1}}\),\(\widehat {{B_1}}\),\(\widehat {{M_2}}\).
b) Chứng minh MN // BC, MP // AC.
c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.
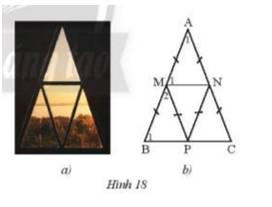
a) Ta thấy tam giác AMN cân tại A do AM = AN
\( \Rightarrow \widehat {{M_1}} = ({180^o} - \widehat {{A_1}}):2 = ({180^o} - {42^o}):2 = {69^o}\)
Ta thấy tam giác PMN = tam giác AMN ( c-c-c )
\( \Rightarrow \widehat {{M_1}} = \widehat {PMN} = {69^o}\) (góc tương ứng )
Mà \( \Rightarrow \widehat {{M_1}} + \widehat {{M_2}} + \widehat {PMN} = {180^o}\)( các góc kề bù )
\( \Rightarrow \widehat {{M_2}} = {180^o} - {69^o} - {69^o} = {42^o}\)
Mà tam giác MPB cân tại M do MB = MP nên
\( \Rightarrow \widehat {{B_1}} = \widehat {MPB}\)
Áp dụng định lí tổng 3 góc trong tam giác
\( \Rightarrow \widehat {{B_1}} = ({180^o} - {42^o}):2 = {69^o}\)
b) Ta thấy \(\widehat {{B_1}}\)và \(\widehat {{M_1}}\)ở vị trí đồng vị và bằng nhau nên
\( \Rightarrow \)MN⫽BC
Vì tam giác PMN = tam giác AMN nên ta có
\( \Rightarrow \widehat {{M_1}} = \widehat {ANM} = \widehat {PMN} = \widehat {MNP}\)( do 2 tam giác cân và bằng nhau )
Mà \(\widehat {MNA}\)và\(\widehat {PMN}\) ở vị trí so le trong
\( \Rightarrow \)MP⫽AC
c) Ta có \(\Delta AMN = \Delta PMN = \Delta MBP(c - g - c)\)(1)
Vì MP⫽AC ( chứng minh trên )
\( \Rightarrow \widehat {MPN} = \widehat {PNC}\) ( 2 góc so le trong ) =\({42^o}\)
\( \Rightarrow \Delta MPN = \Delta NCP(c - g - c)\)(2)
Từ (1) và (2) \( \Rightarrow \) 4 tam giác cân AMN, MBP, PMN, NCP bằng nhau
Trên hình 42 – 43.3 SBT có vẽ trục chính Δ, quang tâm O, hai tiêu điểm F, F’ của một thấu kính, hai tia ló 1, 2 cho ảnh S’ của điểm sáng S. Bằng cách vẽ, hãy xác định điểm sáng S.
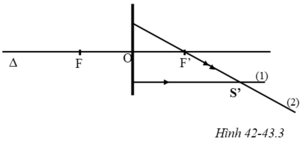
Xác định điểm sáng S bằng cách vẽ như hình 42-43.3a
- Tia ló 1 đi qua tiêu điểm F’, vậy tia tới là tia đi song song với trục chính của thấu kính. Tia ló 2 là tia đi song song với trục chính, vậy tia tới là tia đi qua tiêu điểm của thấu kính.
- Từ I vẽ tia song song với trục chính Δ. Nối K với F. Hai đường trên cắt nhau ở S, ta được điểm sáng S cần vẽ.
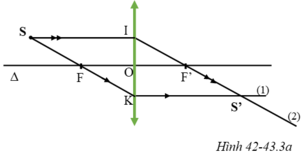
Trên hình 42 – 43.3 SBT có vẽ trục chính Δ, quang tâm O, hai tiêu điểm F, F’ của một thấu kính, hai tia ló 1, 2 cho ảnh S’ của điểm sáng S. Vì sao em biết thấu kính đã cho là hội tụ?
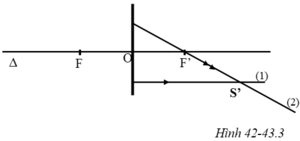
Thấu kính đã cho là thấu kính hội tụ vì chùm tia ló ra khỏi thấu kính cắt nhau tại ảnh S’ và S’ là ảnh thật.
Đề bài :
Cho hình vuông ABCD có S= 200cm2.
Vẽ 1 hình tròn đi qua 4 đỉnh A , B, C, D . Tính S hình O đó.
=> Đường kính hình tròn = 200 : 2 = 100 (cm2)
= 10 cm
S hình tròn = (10 : 2) x (10 : 2) x 3,14 = 78,5 (cm2)
Đáp số: 78,5 cm2
Vẽ 2 đường thẳng xy và mn cắt nhau tại O. Lấy A,B thuộc tia Ox sao cho OA=2cm;OB=5cm. A)Tính AB. B)Vẽ D thuộc tia Oy sao cho O là trung điểm của AD.Tính AD,DB. C)Hình vẽ có mấy đoạn thẳng? Kể tên. D)Kể tên các tia đối nhau chung gốc O?
a: Vì OA<OB
nên A nằm giữa O và B
=>OA+AB=OB
=>AB=3cm
b: AD=2*OA=4cm
DB=4+3=7cm
d: Ox,Oy
Om,On
Bài 1: Vẽ(O;2cm)
a) Lấy A;B;C sao cho OA=OB=OC=2cm
OA;OA là hai tia đối nhau. Xác định vị trí A;B;C vs (O;2cm)
b) Trên hình vẽ có bao nhiêu cung, dây cung?
c) Lấy D;E sao cho OD=1,5cm; OE=3cm. Xác định vị trí D;E với (O;2cm)
Cho đường tròn (O; R) và đường thẳng d không có điểm chung sao cho khoảng cách từ O đến d không quá 2R. Qua diêm M trên d, vẽ các tiếp tuyến MA, MB tới (O) với A, B là các tiếp điểm. Gọi H là hình chiếu vuông góc của O trên d. Vẽ Dây AB cắt OH ở K và cắt OM tại I. Tia OM cắt (O) tại E.a. Chứng minh 5 điểm O,A,M,B,H cùng thuộc 1 đường trònb.Chứng minh OI.OM=R2c. Chứng minh OK.OH = OI.OMd. Tìm vị trí của M trên d để OAEB là hình thoie. Khi M di chuyên trên d. Chứng minh đường thẳng AB luôn đi qua một điểm cố định
Câu 41: Hãy chọn câu trả lời sai.
Cho hình vẽ ta có:
A. ABCD là hình bình hành
B. AB // CD
C. ABCE là hình thang cân
D. BC // AD
Câu 42: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Tứ giác AECH là hình gì?
A. Hình chữ nhật B. Hình bình hành C. Hình thang cân D. Hình thang vuông
Câu 43: Độ dài đường trung tuyến ứng với cạnh huyền của tam giác vuông có các cạnh góc vuông bằng 6cm, 8cm là:
A. 10cm B. 9cm C. 5cm D. 8cm
Câu 44: Hãy chọn câu sai.
A. Tứ giác lồi là tứ giác luôn nằm trong một nửa mặt phẳng có bờ là đường thẳng chứa bất kỳ cạnh nào của tứ giác.
B. Tổng các góc của một tứ giác bằng 1800.
C. Tổng các góc của một tứ giác bằng 3600.
D. Tứ giác ABCD là hình gồm đoạn thẳng AB, BC, CD, DA, trong đó bất kì hai đoạn thẳng nào cũng không nằm trên một đường thẳng.
Câu 45: Cho tứ giác ABCD có góc A= 60 độ, Góc B= 135 độ, góc D= 29 độ. Số đo góc C bằng:
A. 1370 B. 1360 C. 360 D. 1350
Cho hình vuông abc, vẽ góc xAy =90 Ax cắt BC tại M, Ay cắt CD Tại N. Vẽ hbh MANF có AF cắt MN tại O. Cm D, O, B thẳng hàng
Cho hình vẽ:
a c/m AB //CD
b c/m AD//BC
c tính góc C1;C2;C3