Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
∠ A = 60 o , ∠ B = 70 o
b. Tính góc (AIB)
Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
∠ A = 60 o , ∠ B = 70 o
b. Tính góc (AIB)
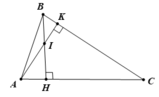
b. Trong tam giác vuông ABH có ∠(ABH) + ∠(AHB) + ∠(BAH) = 180o
Nên ∠(ABH) = 180o - 60o - 90o = 30o ( 1 điểm)
Trong tam giác vuông ABK có (BAK) + (ABK) + (BKA) = 180o
Nên ∠(BAH) = 180o - 70o - 90o = 20o ( 1 điểm)
Trong tam giác ABM có ∠(ABI) + ∠(BAI) + ∠(IAB) = 180onên
∠(AMB) = 180o - 20o - 30o = 130o ( 1 điểm)
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
∠ A = 60 o , ∠ B = 70 o
a. So sánh các cạnh của tam giác ABC
a. Hình vẽ ( 1 điểm)
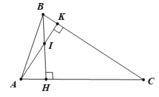
Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)
B. Phần tự luận (6 điểm)
Cho tam giác ABC có hai đường cao AK và BH cắt nhau tại I, biết
∠ A = 60 o , ∠ B = 70 o
a. So sánh các cạnh của tam giác ABC
a. Hình vẽ ( 1 điểm)

Vì ∠A = 60o,B = 70o nên ∠C = 180o - 60o - 70o = 50o ( 1 điểm)
Vì C < A < B ⇒ AB < BC < AC ( 1 điểm)
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O). Hai đường cao AK và CI của tam giác ABC cắt nhau tại H (K ∊ BC, I ∊ AB). a) Chứng minh: Tứ giác BIHK nội tiếp được một đường tròn. b) Đường thẳng AK cắt đường tròn tại D (D khác A). Kẻ đường kính AF. Đường thẳng qua O và vuông góc với BC cắt đường tròn (O) tại E (E thuộc cung nhỏ DF). Chứng minh: AE là tia phân giác của góc DAF
a: góc BIH+góc BKH=180 độ
=>BIHK nội tiếp
b: OE vuông góc BC
=>sđ cung EB=sđ cung EC
=>góc BAE=góc CAE
Xét ΔAKB vuông tại K và ΔACF vuông tại C có
góc ABK=góc AFC
=>ΔAKB đồng dạng với ΔACF
=>góc BAK=góc CAF
=>góc DAE=góc FAE
=>AE là phân giác của góc DAF

`a)` Ta có: `\hat{AHI}=\hat{AKI}=90^o`
`=>` Tứ giác `AHIK` nội tiếp đường tròn đường kính `AI`
`b)` Ta có: `\hat{COB}=2\hat{CAB}` (cùng chắn cung `BC`)
`=>\hat{COB}=2.60^o =120^o=[2\pi]/3(rad)`
`=>` Độ dài cung `BC` nhỏ là: `l=\hat{COB}.R=[2\pi R]/3`
`=>` Diện tích hình quạt giới hạn bởi `2` bán kính `OB;OC` và cung nhỏ `BC` là:
`S=[lR]/2=[R^2]/3`
Cho tam giác ABC có 3 góc nhọn nội tipe61 đường tròn (O;R) hai đường cao BE và CF của tam giác cắt nhau tại H .Kẻ đường kính AK của đường tròn (O;R); Gọi Ià trung điểm của BC.
a) Chứng minh AH=2OI
b) Biết góc BAC=60 độ. tính độ dài dây BC theo R
Cho tam giác ABC nhọn ( AB < AC ) nội tiếp đường tròn (O;R) hai đường cao BE và CF của tam giác ABC cắt nhau tại H và cắt đường tròn (O) lần lượt tại y và x kẻ đường kính AK của (O;R) . Đường thẳng HK cắt (O;R)
tại P
a, c/m tứ giác AEHF nội tiếp
b, c/m PB . PE=PC.PE
Bài 3: Cho tam giác ABC vuông tại A. Đường phân giác BH. Kẻ HK vuông góc với BC tại K. a) Chứng minh ABC = KHC b) Chứng minh BH là đường trung trực của AK. c) Ké CD vuông góc với BH tại D, hai đường thẳng BA và CD cắt nhau tại I. Chứng minh I,H.K thắng hàng. d) Tìm điều kiện của AABC để AADK là tam giác đều.
Cho ∆ABC nhọn (AB < AC) nội tiếp đường tròn (O) có hai đường cao BN và CD cắt nhau tại H. a) Chứng minh tứ giác BDNC nội tiếp, xác định tâm và bán kính đường tròn này. b) Vẽ đường kính AK của đường tròn (O). Chứng minh: BH = CK. c) Chứng minh: AK ⊥ DN
a: góc BDC=góc BNC=90 độ
=>BDNC nội tiếp đường tròn đường kính BC
Tâm là trung điểm của BC
Bán kính là BC/2
b: góc ABK=góc ACK=1/2*sđ cung AK=90 độ
BK vuông góc AB
CH vuông góc AB
=>BK//CH
CK vuông góc AC
BH vuông góc AC
=>CK//BH
Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hbh
=>BH=CK
c: Gọi Ax là tiếp tuyến tại A của (O)
=>góc xAC=góc ABC
=>góc xAC=góc AND
=>Ax//DN
=>AK vuông góc DN