Khai triển 1 9 x 2 - 1 64 y 2 theo hằng đẳng thức ta được
A. x 9 - y 64 x 9 + y 64
B. x 3 - y 4 x 3 + y 4
C. x 9 - y 8 x 9 + y 8
D. x 3 - x 8 x 3 + x 8
Tổng các hệ số nhị thức Niu – tơn trong khai triển ( 1 + x ) 3 n bằng 64. Số hạng không chứa x trong khai triển ( 2 n x + 1 2 n x 2 ) 3 n là
A. 360
B. 210
C. 250
D. 240
Tổng các hệ số nhị thức Niu – tơn trong khai triển (1+x)3n bằng 64. Số hạng không chứa x trong khai triển 2 n x + 1 2 n x 2 3 n là:
A. 360
B. 210
C. 250
D. 240
Ta có: 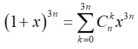
Chọn x=1. Ta có tổng hệ số bằng: ![]()
Lại có: 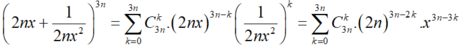
Số hạng không chứa x suy ra ![]()
Do đó số hạng không chứa x là: ![]()
Chọn D.
15. Số hạng chính giữa trong khai triển (3x + 2y)^4 là?
18. Tìm hệ số của x^7 trong khai triển : h(x)= x(2 + 3x)^9 là?
19. Tìm hệ số của x^7 trong khai triển g(x)= (1+x)^7 + (1-x)^8 + (2+x)^9 là?
15/ Mũ 4=> có 4+1=5 số hạng=> số hạng chính giữa là: \(C^2_4.3^{4-2}.x^2.2^2y^2=58x^2y^2\)
18/ \(x.x^k=x^7\Rightarrow k=6\)
\(C^6_9.3^6.2^3=489888\)
19/ \(C^7_7+C^7_8.\left(-1\right)^7+C^7_9.2^2=...\)
Tổng các hệ số nhị thức Niu – tơn trong khai triển ( 1 + x ) 3 n bằng 64. Số hạng không chứa x trong khai triển ( 2 n x + 1 2 n x 2 ) 3 n là
A. 360
B. 210
C. 250
D. 240
Tổng các hệ số nhị thức Niu – tơn trong khai triển 1 + x 3 n bằng 64. Số hạng không chứa x trong khai triển 2 n x + 1 2 n x 2 3 n là
A. 360
B. 210
C. 250
D. 240
tổng các hệ số nhị thức niuton trong khai triển \(\left(2nx+\frac{1}{2nx^2}\right)^{3n}\) bằng 64 . số hạng không chứa x trong khai triển là bao nhiêu ?
ta có : \(\left(2nx+\dfrac{1}{2nx^2}\right)^{3n}=\sum\limits^{3n}_{k=0}C^k_{3n}\left(2nx\right)^{3n-k}\left(\dfrac{1}{2nx^2}\right)^k\)
\(=\sum\limits^{3n}_{k=0}C^k_{3n}2^{3n-2k}\left(n\right)^{3n-2k}\left(x\right)^{3n-3k}\)
\(\Rightarrow\) tổng hệ số bằng : \(C^0_{3n}+C_{3n}^1+C^2_{3n}+...+C^{3n}_{3n}=64\)
\(\Leftrightarrow\left(1+1\right)^{3n}=64\Leftrightarrow2^{3n}=2^6\Rightarrow n=2\)
để có số hạng không chữa \(x\) không khai triển thì \(3n-3k=0\Leftrightarrow n=k\)
\(\Rightarrow\) hệ số của số hạng không chữa \(x\) là \(C^2_6.2^2.2^2=240\)
vậy ...........................................................................................................................
Khai triển các hằng đẳng thức sau
1)x^3-1
2)27x^3-64
3)8x^3+1
1) \(x^3-1=x^3-1^3=\left(x-1\right)\left(x^2+x+1\right)\)
2) \(27x^3-64=\left(3x\right)^3-4^3=\left(3x-4\right)\left(9x^2+12x+4\right)\)
3) \(8x^3+1=\left(2x\right)^3+1^3=\left(2x+1\right)\left(4x^2-2x+1\right)\)
Bài 1 : \(x^3-1=\left(x-1\right)\cdot\left(x^2+x+1\right)\)
Bài 2 : \(27x^3-64=27x^3-4^3=\left(3x-4\right)\cdot\left(9x^2+12x+16\right)\)
Bài 3 : \(8x^3+1=\left(2x+1\right)\cdot\left(4x^2-2x+1\right)\)
Tổng hai lập phương:Hiệu hai lập phương:
8. Trong khai triển (8a^2 - 1/2b)^6 hệ số của số hạng chứa a^9.b^3 là?
9. Trong khai triển ( x + 8/x^2)^9 số hạng ko chứa x là?
A. 4308
B. 86016
C. 84
D. 43008
Câu 8 là \(\left(8a^2-\dfrac{1}{2}b\right)^6\) hay \(\left(8a^2-\dfrac{1}{2b}\right)^6\) bạn? (tốt nhất là bạn dùng tính năng gõ công thức toán để đăng đề, hoặc chụp hình gửi đề trực tiếp lên, hiện nay hoc24 đã cho đăng đề bằng hình ảnh)
9.
\(\left(x+8.x^{-2}\right)^9=\sum\limits^9_{k=0}C_9^kx^{9-k}.8^k.x^{-2k}=\sum\limits^9_{k=0}C_9^k8^kx^{9-3k}\)
Số hạng ko chứa x \(\Rightarrow9-3k=0\Rightarrow k=3\)
Số hạng đó là: \(C_9^3.8^3=...\)
1. Tìm hệ số của số hạng \(x^4\) trong khai triển \(\left(x-3\right)^9\)
2. Tìm hệ số của số hạng chứa \(x^{12}y^{13}\) trong khai triển \(\left(2x+3y\right)^{25}\)
3. Tìm hệ số của số hạng chứa \(x^4\) trong khai triển \(\left(\dfrac{x}{3}-\dfrac{3}{x}\right)^{12}\)
4. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x^2-\dfrac{1}{x}\right)^6\)
5. Tìm hệ số của số hạng không chứa x trong khai triển \(\left(x+\dfrac{1}{x^4}\right)^{10}\)
Tìm số hạng chứa x^9 trong khai triển (x^2+x-1)^6
Số hạng trong khai triển có dạng :
\(T_{k+1}=C_6^k.\left(x^2\right)^{6-k}.\left(x^{-1}\right)^k\)
\(=C_6^k.x^{12-2k}.x^{-k}\)
\(=C_6^k.x^{12-3k}\)
Số hạng chứa \(x^9\): \(\Leftrightarrow x^{12-3k}=x^9\)
\(\Leftrightarrow12-3k=9\)
\(\Leftrightarrow3k=12-9\)
\(\Leftrightarrow3k=3\)
\(\Leftrightarrow k=1\)
Hệ số của số hạng chứa \(x^9\)là : \(T_2=C^1_6=6\)