Cho hình thang vuông ABCD có A ⏞ = D ⏞ = 90 ∘ , AB=AD=2, CD=2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.
A. 8 π cm 3
B. 40 π 3 c m 3
C. 8 π 3 c m 3
D. 16 π 3 c m 3
Những câu hỏi liên quan
1, cho hình thang vuông ABCD có A = D = 90 độ , AB = AD =2 cm , CD= 4cm . tính B , C của hình thang.
2, cho hình thangg vuông ABCD có A = D =90 độ , CD = BC =2AB . Tính góc ABC.
\(2,\)
Kẻ BH vuông góc với CD tại H
Xét hai tam giác BDH và BCH:
+) BH là cạnh chung
+) Góc BHD = góc BHC = 90 độ
+) DH = CH
=> Tam giác BDH = tam giác HCH (c.g.c)
=> BD = BC
Khác: DC = BC
=> BC = CD = DB => Tam giác BCD đều => Góc C = 60 độ
Mà: AB // CD => Góc B + góc C = 180 độ => Góc B = góc ABC = 180 độ - 60 độ = 120 độ
Cho hình thang ABCD có ∠A = ∠D = 90◦ CD = 2AD = 2AB, cho AC = 2√5.
a) Tính ∠ACD, AB, AD, CD.
b) Vẽ DH⊥AC. Tính DH.
a: Xét ΔADC vuông tại D có
\(\tan\widehat{ACD}=\dfrac{AD}{DC}=\dfrac{1}{2}\)
nên \(\widehat{ACD}\simeq27^0\)
Áp dụng định lí Pytago vào ΔACD vuông tại D, ta được:
\(AC^2=AD^2+DC^2\)
\(\Leftrightarrow5\cdot AD^2=20\)
\(\Leftrightarrow AD=2\left(cm\right)\)
\(\Leftrightarrow DC=4\left(cm\right)\)
b: Xét ΔADC vuông tại D có DH là đường cao ứng với cạnh huyền AC nên ta có:
\(DH\cdot AC=DC\cdot DA\)
\(\Leftrightarrow DH\cdot2\sqrt{5}=2\cdot4=8\)
hay \(DH=\dfrac{4\sqrt{5}}{5}\left(cm\right)\)
Đúng 0
Bình luận (0)
Cho hình thang ABCD có ∠A = ∠D = 90◦,CD = 2AD = 2AB, cho AC = 2√5.
a) Tính ∠ACD, AB, AD, CD.
b) Vẽ DH⊥AC. Tính DH.
a.
\(tan\widehat{ACD}=\dfrac{AD}{CD}=\dfrac{1}{2}\Rightarrow\widehat{ACD}\approx26^034'\)
Áp dụng Pitago cho tam giác vuông ACD:
\(AC^2=AD^2+CD^2\Leftrightarrow\left(2\sqrt{5}\right)^2=AD^2+\left(2AD\right)^2\)
\(\Rightarrow AD^2=4\Rightarrow AD=2\Rightarrow AB=AD=2\)
\(CD=2AB=4\)
b.
Áp dụng hệ thức lượng trong tam giác vuông ACD:
\(DH.AC=AD.CD\)
\(\Rightarrow DH=\dfrac{AD.CD}{AC}=\dfrac{4.2}{2\sqrt{5}}=\dfrac{4\sqrt{5}}{5}\)
Đúng 0
Bình luận (0)
cho hình thang vuông abcd có : a=d=90 AB = 2 CD ; AD = CD .M là trung điểm AD . Tính góc BMC
Cho hình thang ABCD có góc A =góc D = 90°,CD = 2AD = 2AB, cho AC = 25.
a) Tính góc ACD.
b) Tính AB, AD,CD.
c) Vẽ DH vuông góc AC. Tính DH và chứng minh góc ABH = góc ACB.
a) Xét tam giác \(ADC\)vuông tại \(D\):
\(tan\widehat{ACD}=\frac{AD}{DC}=\frac{1}{2}\Rightarrow\widehat{ACD}=arctan\frac{1}{2}\)
b) Xét tam giác \(ADC\)vuông tại \(D\):
\(AC^2=AD^2+DC^2=AD^2+4AD^2=5AD^2\)
\(\Leftrightarrow AD=\sqrt{\frac{AC^2}{5}}=\sqrt{\frac{25^2}{5}}=5\sqrt{5}\left(cm\right)\)
\(AB=AD=5\sqrt{5}\left(cm\right),CD=2AD=10\sqrt{5}\left(cm\right)\).
c) Xét tam giác \(ADC\)vuông tại \(D\):
\(DH=\frac{AD.DC}{AC}=\frac{10\sqrt{5}.5\sqrt{5}}{25}=10\left(cm\right)\)
\(AH=\frac{AD^2}{AC}=\frac{AB^2}{AC}\Leftrightarrow\frac{AB}{AC}=\frac{AH}{AB}\)
Xét tam giác \(ABH\)và tam giác \(ACB\):
\(\widehat{A}\)chung
\(\frac{AB}{AC}=\frac{AH}{AB}\)
suy ra \(\Delta ABH~\Delta ACB\left(c.g.c\right)\)
\(\Rightarrow\widehat{ABH}=\widehat{ACB}\)
Cho hình thang vuông ABCD có
A
^
D
^
90
o
,
AB
AD
2
cm
,
CD
2
AB
.
Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB A.
40
π
3...
Đọc tiếp
Cho hình thang vuông ABCD có A ^ = D ^ = 90 o , AB = AD = 2 cm , CD = 2 AB . Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB
A. 40 π 3 cm 3
B. 16 π 3 cm 3
C. 8 πcm 3
D. 8 π 3 cm 3
Đáp án A
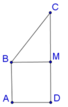
Ta có thể tích khối tròn xoay tạo thành bằng hiệu thể tích hình trụ bán kính đáy AD, chiều cao CD trừ cho thể tích nón đỉnh B, bán kính đáy BM chiều cao CM.
Ta có
Đúng 0
Bình luận (0)
Cho hình thang vuông ABCD có
A
^
D
^
90
o
, ABAD2cm, CD2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.
Đọc tiếp
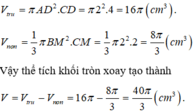
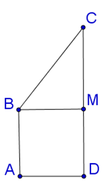
Cho hình thang vuông ABCD có A ^ = D ^ = 90 o , AB=AD=2cm, CD=2AB. Tính thể tích khối tròn xoay tạo thành khi quay hình thang quanh trục là cạnh AB.
Chọn B
Ta có thể tích khối tròn xoay tạo thành bằng hiệu
thể tích hình trụ bán kính đáy AD, chiều cao
CD trừ cho thể tích nón đỉnh B, bán kính đáy
BM chiều cao CM.
Ta có:
Đúng 0
Bình luận (0)
cho hình thang vuông ABCD ( AB//CD ; AD vuông góc AB ) có CD= 2AB . DH vuông góc AC . M ;N là trung điểm HD ; HC . Chứng minh :
a, MN = AB .
b, ABNM là hình bình hành
c , M là trực tâm tam giác AND .
d, góc BND =90 độ
cần gấp nha mn !
ai nhanh mik tick cho :>>>
Đúng 0
Bình luận (0)
Bài 1: Hình thang ABCD (AB//CD) có AB=AD+BC. Chứng minh rằng các tia phân giác của các góc C và D gặp nhau tại 1 điểm thuộc đáy AB
Bài 2: Hình thang vuông ABCD (góc A = góc D= 90°)có AB =4cm, CD=9cm, BC=13cm. Tính AD
Bài 3: hình thang vuông ABCD (góc A=góc D=90°)có AB =9cm,CD=15cm, AC=17cm. Tính độ dài cạnh bên
