Question

Cho hình thang ABCD có ∠A = ∠D = 90◦,CD = 2AD = 2AB, cho AC = 2√5.
a) Tính ∠ACD, AB, AD, CD.
b) Vẽ DH⊥AC. Tính DH.

Answer 1

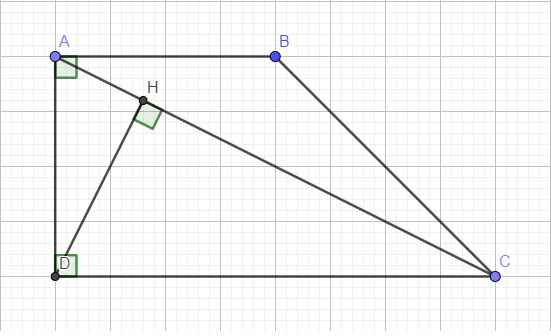
a.

\(tan\widehat{ACD}=\dfrac{AD}{CD}=\dfrac{1}{2}\Rightarrow\widehat{ACD}\approx26^034'\)

Áp dụng Pitago cho tam giác vuông ACD:

\(AC^2=AD^2+CD^2\Leftrightarrow\left(2\sqrt{5}\right)^2=AD^2+\left(2AD\right)^2\)

\(\Rightarrow AD^2=4\Rightarrow AD=2\Rightarrow AB=AD=2\)

\(CD=2AB=4\)

b.

Áp dụng hệ thức lượng trong tam giác vuông ACD:

\(DH.AC=AD.CD\)

\(\Rightarrow DH=\dfrac{AD.CD}{AC}=\dfrac{4.2}{2\sqrt{5}}=\dfrac{4\sqrt{5}}{5}\)

Answer 2