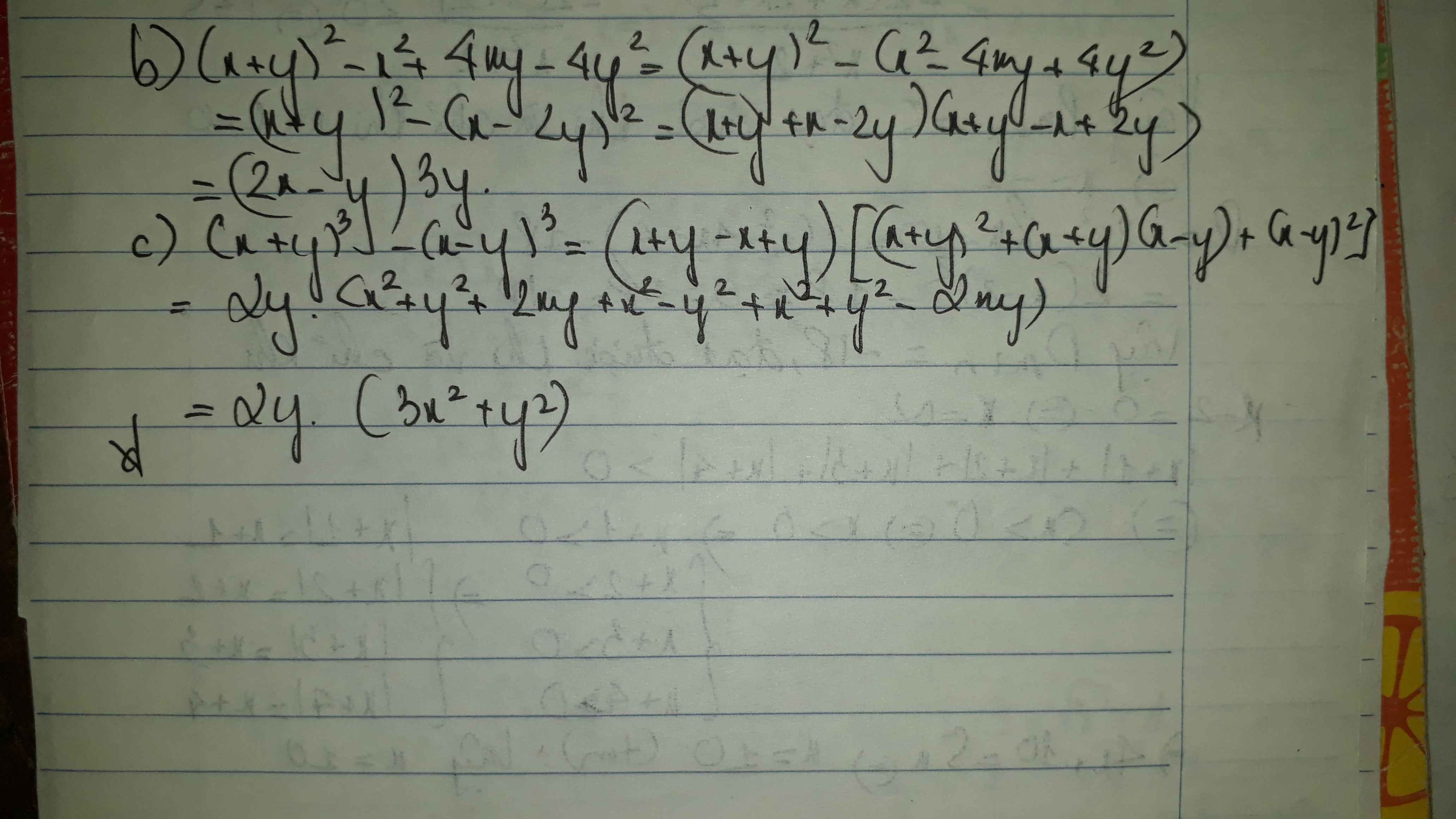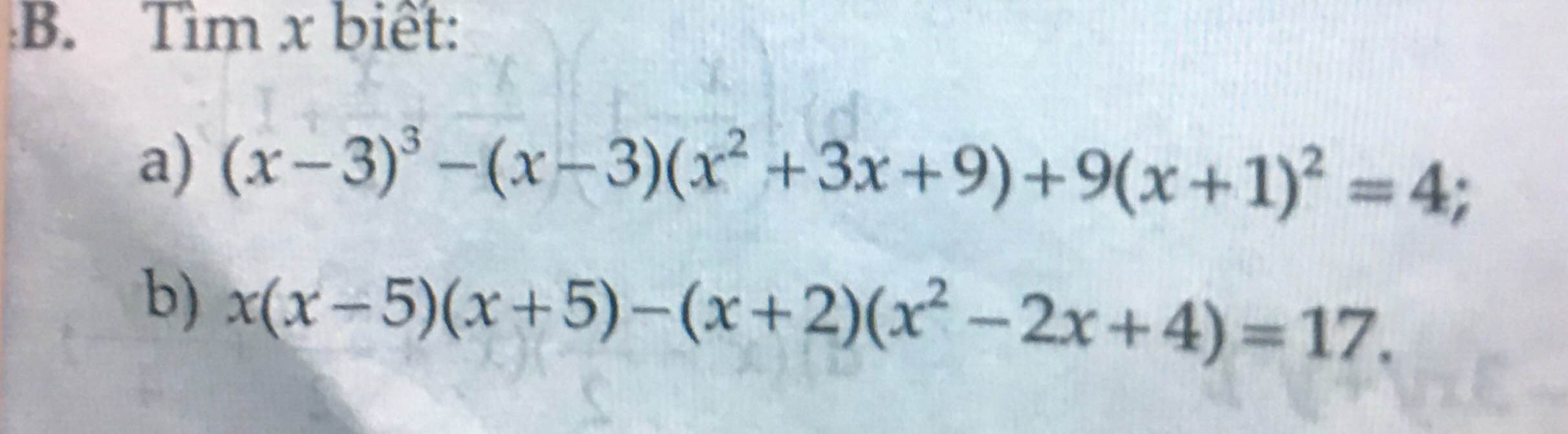
a: Ta có: \(\left(x-3\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+9\left(x+1\right)^2=4\)

\(\Leftrightarrow x^3-9x^2+27x-27-x^3+27+9x^2+18x+9=4\)

\(\Leftrightarrow45x=-5\)

hay \(x=-\dfrac{1}{9}\)

b: Ta có: \(x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=17\)

\(\Leftrightarrow x^3-25x-x^3-8=17\)

\(\Leftrightarrow-25x=25\)

hay x=-1

Câu 1.

Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)

\(;a_i\ne a_j\)

Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.

5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)

\(\Rightarrow\)Có \(A_8^5\) cách.

Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.

c

Bài 1:

Ta có : 1 mol muối RCO₃ (có khối lượng = R + 60n) chuyển thành 1 mol RCl_n (có khối lượng = R + 71n)

=> khối lượng tăng = 71n – 60n = 11n gam

=> Khi chuyển 1 mol gốc CO₃ thành 2 mol gốc Cl và tạo ra 1 mol CO₂ thì khối lượng tăng 11 gam

a) Ta có công thức tính nhanh sau : \(m_{muốiclorua}=n_{muốicacbonat}+11.n_{CO_2}\)

=> \(n_{CO_2}=\dfrac{11,1-10}{11}=0,1\left(mol\right)\)

=> \(V_{CO_2}=0,1.22,4=2,24\left(l\right)\)

b) \(MCO_3+2HCl\rightarrow MCl_2+CO_2+H_2O\)

\(n_{HCl}=2n_{CO_2}=0,2\left(mol\right)\)

=> \(m_{ddHCl}=\dfrac{0,2.36,5}{3,65\%}=200\left(g\right)\)

c) \(m_{ddsaupu}=10+200-0,1.44=205,6\left(g\right)\)

\(C\%_{muối}=\dfrac{11,1}{205,6}.100=5,4\%\)

d) \(n_{MCO_3}=n_{MCl_2}\)

=> \(\dfrac{10}{M+60}=\dfrac{11,1}{M+71}\)

=> \(M=40\left(Ca\right)\)

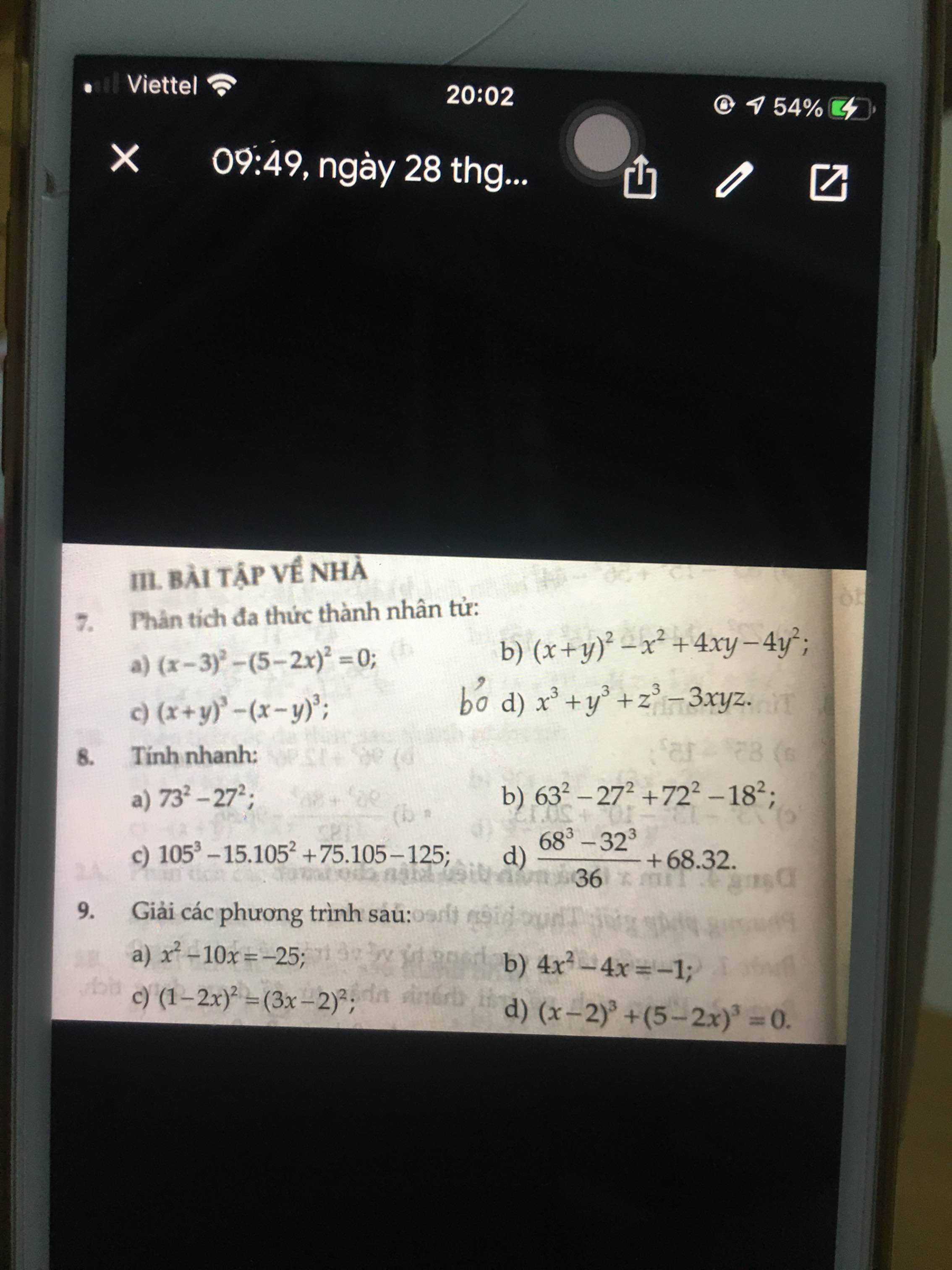
Bài 9:

a: Ta có: \(x^2-10x=-25\)

\(\Leftrightarrow x^2-10x+25=0\)

\(\Leftrightarrow x-5=0\)

hay x=5

b: ta có: \(4x^2-4x=-1\)

\(\Leftrightarrow4x^2-4x+1=0\)

\(\Leftrightarrow2x-1=0\)

hay \(x=\dfrac{1}{2}\)

c: Ta có: \(\left(2x-1\right)^2=\left(3x-2\right)^2\)

\(\Leftrightarrow\left(3x-2\right)^2-\left(2x-1\right)^2=0\)

\(\Leftrightarrow\left(3x-2-2x+1\right)\left(3x-2+2x-1\right)=0\)

\(\Leftrightarrow\left(x-1\right)\left(5x-3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{3}{5}\end{matrix}\right.\)

Bài 7a đề sai bạn nhé.

Bài 7:

a. \(\left(x-3\right)^2-\left(5-2x\right)^2=\left(x-3-5+2x\right)\left(x-3+5-2x\right)=\left(3x-8\right)\left(2-x\right)\)

b. \(\left(x+y\right)^2-x^2+4xy-4y^2=\left(x+y\right)^2-\left(x-2y\right)^2=\left(x+y-x+2y\right)\left(x-y+x-2y\right)=3y\left(2x-3y\right)\)

c. \(\left(x+y\right)^3-\left(x-y\right)^3=\left(x+y-x+y\right)\left[\left(x+y\right)^2+\left(x+y\right)\left(x-y\right)+\left(x-y\right)^2\right]=2y\left(3x^2+y^2\right)\)

d. \(x^3+y^3+z^3-3xyz\)

\(=\left(x+y\right)^3-3x^2y-3xy^2+z^3-3xyz\)

\(=\left[\left(x+y\right)^3+z^3\right]-3xy\left(x+y+z\right)\)

\(=\left(x+y+z\right)\left[\left(x+y\right)^2-z\left(x+y\right)+z^2\right]-3xy\left(x+y+z\right)\)

\(=\left(x+y+z\right)\left(x^2+y^2+z^2-xy-xz-yz\right)\)