Cho mẫu số liệu thống kê: {5;2;1;6;7;5;4;5;9}. Mốt M 0 của mẫu số liệu trên bằng bao nhiêu?
A. 3
B. 5
C. 9
D. 7
Cho mẫu số liệu thống kê {6;4;4;1;9;10;7} . Số liệu trung vị của mẫu số liệu thống kê trên là:
A. 1
B. 6
C. 4
D. 10
Đáp án B.
Sắp thứ tự các số liệu thống kê thành một dãy không giảm là:
1 4 4 6 7 9 10
Vậy số trung vị là M e = 6
Chú ý: Cách tìm số trung vị M e = 6
+ Sắp thứ tự các số liệu thống kê thành 1 dãy không giảm (không tăng).
+ Nếu số phần tử lẻ thì M e = 6 là số đứng giữa dãy.
+ Nếu số phần tử chẵn thì M e = 6 là trung bình cộng của 2 số đứng giữa dãy.
Thống kê số huy chương bốn quốc gia dẫn đầu SEA Games 31 được cho trong bảng số liệu sau:
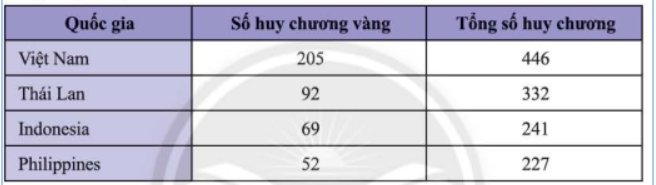
Hãy chuyển dữ liệu đã cho vào bảng thống kê theo mẫu dưới đây và vào biểu đồ cột kép tương ứng.

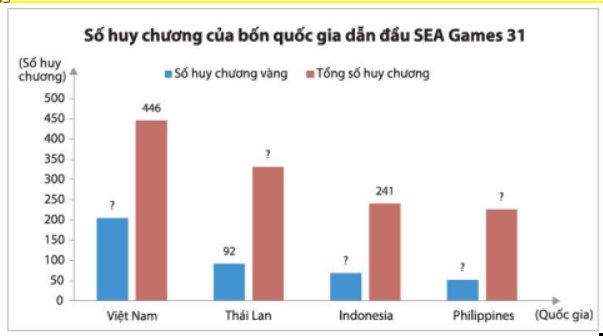
Điền số vào bảng: 446 92 69 227
Biểu đồ; 205 322 69 52 227
cho bảng thống kê điểm lớp 10A1
| điểm | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| số hs | 2 | 3 | 7 | 18 | 3 | 2 | 4 | 1 |
tìm độ lệch chuẩn của mẫu số liệu trên
Cho dãy số liệu thống kê: 5; 6; 7; 8; 9. Phương sai của dãy số liệu thống kê trên là:
A. 10
B. 7
C. 6
D.2
Đáp án D.
+ Trung bình cộng của dãy là x ¯ = 7
+ Phương sai của dãy số liệu thống kê là:
S 2 = 1 5 - 7 2 + 1 . 6 - 7 2 + 1 . 7 - 7 2 + 1 . 8 - 7 2 + 1 . 5 5 S 2 = 10 5 = 2
Cho dãy số liệu thống kê : 1, 2, 3, 4, 5, 6, 7
Hỏi phương sai của các số liệu thống kê đã cho là bao nhiêu ?
là 4 vì \(S^2=\dfrac{3^2+2^2+1^2+0^2+1^2+2^2+3^2}{7}=4\)
Số liệu thống kê điểm kiểm tra môn Toán của học sinh lớp 10A được cho trong bảng sau:
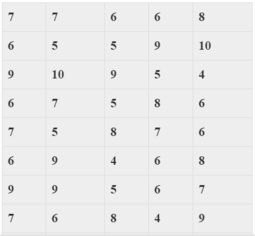

Đơn vị điều tra và kích thước mẫu của bảng số liệu trên là:
A. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44
B. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45
C. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45
D. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44
Chọn A.
Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A
Liệt kê số điểm của 44 học sinh lớp 10A nên kích thước mẫu của số liệu là 44.
Cho dãy số liệu thống kê: 21, 23, 24, 25, 22, 20, 27, 28. Số trung bình cộng của dãy số liệu thống kê đã cho là
A. 23,57
B. 23,75
C. 19
D. 22,57
Chọn B.
Số trung bình của dãy số liệu thống kê đã cho là:
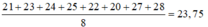
Một cửa hàng đã thống kê số ba lỗ bán được mỗi ngày trong tháng 9 với kết quả cho như sau:

Hãy chia mẫu số liệu trên thành 5 nhóm, lập tần số ghép nhóm, hiệu chỉnh bảng và xác định giá trị đại diện cho mỗi nhóm.
Tham khảo:
Khoảng biến thiên của mẫu số liệu trên là \(R = 29 - 10 = 19\).
Độ dài mỗi nhóm \(L > \frac{R}{k} = \frac{{19}}{5} = 3,8\).
Ta chọn \(L = 4\) và chia dữ liệu thành các nhóm: \(\left[ {10;14} \right),\left[ {14;18} \right),\left[ {18;22} \right),\left[ {22;26} \right),\left[ {26;30} \right)\).
Khi đó ta có bảng tần số ghép nhóm sau:

Số liệu thống kê kết quả 5 bài kiểm tra môn Toán của bạn Dũng là: 8 6 7 5 9 (3) (xem Bảng 4).
Số trung bình cộng của mẫu số liệu (3) là: \(\overline x = \frac{{8 + 6 + 7 + 5 + 9}}{5} = 7\)
a) Tính các độ lệch sau: (8 – 7); (6 – 7); (7 – 7); (5 – 7); (9 – 7).
b) Tính bình phương các độ lệch và tính trung bình cộng của chúng.
a) Ta có: \(8 - 7 = 1;6 - 7 = - 1;7 - 7 = 0;5 - 7 = - 2;9 - 7 = 2\)
b) +) Bình phương các độ lệch là: \({(8 - 7)^2} = 1;{(6 - 7)^2} = 1;{(7 - 7)^2} = 0;{(5 - 7)^2} = 4;{(9 - 7)^2} = 4\)
+) Trung bình cộng của bình phương các độ lệch là:
\({s^2} = \frac{{{{(8 - 7)}^2} + {{(6 - 7)}^2} + {{(7 - 7)}^2} + {{(5 - 7)}^2} + {{(9 - 7)}^2}}}{5} = 2\)