Trong các điểm có tọa độ cho sau đây, điểm nào thuộc miền nghiệm của bất phương trình x + 3 y - 2 ≥ 0 2 x + y + 1 ≤ 0 ?
A. (0;1)
B. (-1;1)
C. (1;3)
D. (-1;0)
Trong các điểm có tọa độ cho sau đây, điểm nào thuộc miền nghiệm của bất phương trình x + 3 y - 2 ≥ 0 2 x + y + 1 ≤ 0 ?
A. (0;1)
B.(-1;1)
C. (1;3)
(-1:0)
Thay tọa độ các điểm vào từng bất phương trình ta thấy, điểm (-1 ; 1) thỏa mãn cả hai bất phương trình : - 1 + 3 . 1 - 2 ≥ 0 ; 2 . - 1 + 1 + 1 ≤ 0
Do đó, điểm (-1; 1) thuộc miền nghiệm của bất phương trình đã cho.
Chọn B
Điểm O(0;0) thuộc miền nghiệm của bất phương trình nào sau đây?
A. x + 3y + 2 ≤ 0
B. x + y + 2 ≤ 0
C. 2 x + 5 y - 2 ≥ 0
D. 2 x + y + 2 ≥ 0
Dễ thấy O(0;0) thỏa mãn bất phương trình 2 x + y + 2 ≥ 0 , không thỏa mãn các bất phương trình còn lại. Đáp án là D.
Điểm O (0;0) thuộc miền nghiệm của hệ bất phương trình nào sau đây?
A. x + 3 y - 6 > 0 2 x + y + 4 > 0
B. x + 3 y - 6 > 0 2 x + y + 4 < 0
C. x + 3 y - 6 < 0 2 x + y + 4 > 0
D. x + 3 y - 6 < 0 2 x + y + 4 < 0
Thay tọa độ của điểm O (0;0) vào các bất phương trình ta thấy O thuộc miền nghiệm của bất phương trình x + 3 y - 6 < 0 và 2 x + y + 4 > 0 .
Do đó O thuộc miền nghiệm của hệ bất phương trình x + 3 y - 6 < 0 2 x + y + 4 > 0 .
Đáp án là C.
Cho hệ bất phương trình bậc nhất hai ẩn \(\left\{ \begin{array}{l}x + y > 2\\x - y \le 1\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ bất phương trình đã cho?
A. (1;1)
B. (2;0)
C. (3;2)
D. (3;-2)
(1;1) không thuộc miền nghiệm vì 1+1=2>2 (Vô lý) => Loại A
(2;0) không thuộc miền nghiệm vì 2+0=2>2 (Vô lý) => Loại B
(3;2) thuộc miền nghiệm vì: 3+2 =5 > 2 (đúng) và \(3 - 2 = 1 \ge 1\) (đúng)
(3;-2) không thuộc miền nghiệm vì 3+ (-2)=1>2 (Vô lý) => Loại D
Chọn C.
Cho hệ bất phương trình \(\left\{ \begin{array}{l}x - y < - 3\\2y \ge - 4\end{array} \right.\). Điểm nào sau đây thuộc miền nghiệm của hệ đã cho?
A. (0;0)
B. (-2;1)
C. (3;-1)
D. (-3;1)
Thay tọa độ điểm (0;0) vào ta được: \(\left\{ \begin{array}{l}0 - 0 < - 3\left( {ktm} \right)\\2.0 \ge - 4\left( {tm} \right)\end{array} \right.\)
=> Loại A
Thay tọa độ điểm (-2;1) vào ta được: \(\left\{ \begin{array}{l} - 2 - 1 < - 3\left( {ktm} \right)\\2.1 \ge - 4\left( {tm} \right)\end{array} \right.\)
=> Loại B.
Thay tọa độ điểm (3;-1) vào ta được: \(\left\{ \begin{array}{l}3 - \left( { - 1} \right) < - 3\left( {ktm} \right)\\2.\left( { - 1} \right) \ge - 4\left( {tm} \right)\end{array} \right.\)
Loại C
Thay tọa độ điểm (-3;1) vào ta được: \(\left\{ \begin{array}{l} - 3 - 1 < - 3\left( {tm} \right)\\2.1 \ge - 4\left( {tm} \right)\end{array} \right.\)
Chọn D.
Miền nghiệm của bất phương trình x+3y-2<0 là nửa mặt phẳng chứa điểm nào trong các điểm sau?
A. A(1;1)
B.B(-1;0)
C. C(0;1)
D. D(2;1)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d có phương trình x - 1 3 = y + 2 2 = z - 3 - 4 . Điểm nào sau đây không thuộc đường thẳng d?
![]()
![]()
![]()
![]()
Điểm O(0; 0) thuộc miền nghiệm của bất phương trình nào sau đây?
A. x+3y+2≤0x+3y+2≤0
B. x+y+2≤0x+y+2≤0
C. 2x+5y−2≥02x+5y−2≥0
D. 2x+y+2≥0
Đáp án D là đáp án đúng
Thế tọa độ O lần lượt vào các đáp án thì A: \(2\le0\) (sai), B: \(2\le0\) (sai), C:\(-2\ge0\) (sai)
D: \(2\ge0\) (đúng)
Biểu diễn miền nghiệm của các bất phương trình sau trên mặt phẳng tọa độ Oxy:
a) \( - x + 2 + 2(y - 2) < 2(1 - x)\)
b) \(3(x - 1) + 4(y - 2) < 5x - 3\)
Tham khảo:
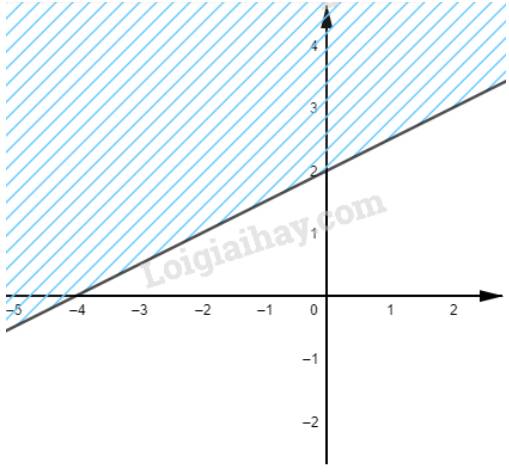
a) Ta có: \( - x + 2 + 2(y - 2) < 2(1 - x) \Leftrightarrow 2y + x - 4 < 0\)
Vẽ đường thẳng \(\Delta :2y + x - 4 = 0\) đi qua hai điểm \(A(2;1)\) và \(B\left( {0;2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(2.0 + 0 - 4 = - 4 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
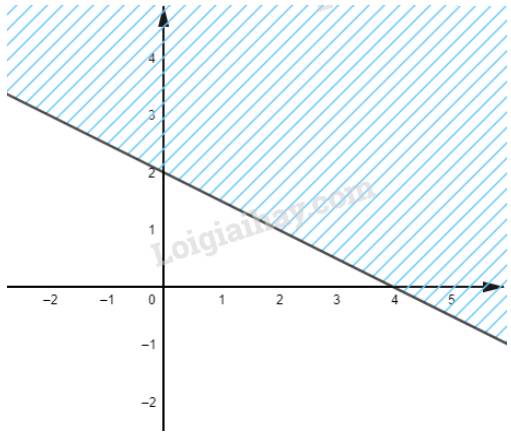
b) Ta có: \(3(x - 1) + 4(y - 2) < 5x - 3 \Leftrightarrow 4y - 2x - 8 < 0 \Leftrightarrow 2y - x - 4 < 0\)
Vẽ đường thẳng \(\Delta :2y - x - 4 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {1; - 2} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(2.0 - 0 - 4 = - 4 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng không kể bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)