Hình vuông ABCD có A(2;1), C(4;3). Tọa độ của đỉnh B có thể là:
A. (-2;-3)
B. (1;4)
C. (-4;-1)
D. (-3;-2)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O , cạnh a , SA vuông góc ABCD , SA =a√2
a) CM : BD vuông góc SAC
b) tính góc giữa SC và mp ABCD
25.
\(\lim\dfrac{3.5^n+7.7^n+9}{6.5^n+9.7^n-3}=\lim\dfrac{7^n\left[3\left(\dfrac{5}{7}\right)^n+7+9.\left(\dfrac{1}{7}\right)^n\right]}{7^n\left[6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n\right]}\)
\(=\lim\dfrac{3\left(\dfrac{5}{7}\right)^n+7+9\left(\dfrac{1}{7}\right)^n}{6\left(\dfrac{5}{7}\right)^n+9-3\left(\dfrac{1}{7}\right)^n}=\dfrac{3.0+7+9.0}{6.0+9-3.0}=\dfrac{7}{9}\)
26.
\(\lim\left(n-\sqrt{n^2-4n}\right)=\lim\dfrac{\left(n-\sqrt{n^2-4n}\right)\left(n+\sqrt{n^2-4n}\right)}{n+\sqrt{n^2-4n}}\)
\(=\lim\dfrac{4n}{n+\sqrt{n^2-4n}}=\lim\dfrac{4n}{n\left(1+\sqrt{1-\dfrac{4}{n}}\right)}\)
\(=\lim\dfrac{4}{1+\sqrt{1-\dfrac{4}{n}}}=\dfrac{4}{1+\sqrt{1-0}}=2\)
26.
\(u_1=5\)
\(u_n=405=u_1.q^{n-1}\Rightarrow q^{n-1}=\dfrac{405}{5}=81\)
\(\Rightarrow q^n=81q\)
Do \(S_n=\dfrac{u_1\left(1-q^n\right)}{1-q}\Rightarrow605=\dfrac{5\left(1-81q\right)}{1-q}\)
\(\Rightarrow605-605q=5-405q\)
\(\Rightarrow q=3\)
27.
a.
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow BD\perp\left(SAC\right)\)
b.
Do \(SA\perp\left(ABCD\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABCD)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABCD)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
Cho hình vuông ABCD có cạnh bằng a. Người ta dựng hình vuông A1B1C1D1 có cạnh bằng 1/2 đường chéo của hình vuông ABCD, dựng hình vuông A2B2C2D2 có cạnh bằng 1/2 đường chéo của hình vuông A1B1C1D1 và cứ tiếp tục như vậy. Giả sử cách dựng trên có thể tiến ra vô hạn. Nếu tổng diện tích của tất cả hình vuông ABCD,A1B1C1D1,A2B2C2D2,... bằng 8 thì a bằng bao nhiêu?
Xét dãy số \(u_n=S_{A_nB_nC_nD_n}\). Ta có \(u_1=a^2\)
Ta xét hình vuông có cạnh \(x\) (diện tích là \(x^2\)). Khi đó nửa độ dài đường chéo của hình vuông này sẽ là \(\dfrac{x}{\sqrt{2}}\). Khi đó diện tích của hình vuông mới là \(\left(\dfrac{x}{\sqrt{2}}\right)^2=\dfrac{x^2}{2}\) bằng 1 nửa diện tích hình vuông ban đầu. Như vậy, ta có mối quan hệ truy hồi: \(u_{n+1}=2u_n\). Dễ thấy đây là một cấp số nhân.
Ta có \(\left(u_n\right):\left\{{}\begin{matrix}u_1=a^2\\u_{n+1}=2u_n\end{matrix}\right.\)
\(\Rightarrow S_n=\sum\limits^{\infty}_{i=1}u_i=a^2\left(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}\right)=2a^2\)
(Đẳng thức quen thuộc \(\sum\limits^{\infty}_{i=0}\dfrac{1}{2^i}=2\))
Cho \(S_n=8\) \(\Rightarrow2a^2=8\Leftrightarrow a=2\).
Vậy \(a=2\) thỏa mãn ycbt.
Cho hình chóp sabcd có abcd là hình thang vuông tại a,d. Ab=2a, ad=cd=a. Sa=a√2, sa vuông góc abcd a, (sb,(abcd))=? (Sc,(abcd)=? b, kẻ ah vuông góc sc tại h. Ak vuông góc sd tại k (Ah,(sad))=? (Sb,(sac)=?
a.
\(SA\perp\left(ABCD\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABCD)
\(\Rightarrow\widehat{SBA}=\left(SB;\left(ABCD\right)\right)\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{\sqrt{2}}{2}\Rightarrow\widehat{SBA}\approx35^016'\)
Tương tự \(SA\perp\left(ABCD\right)\Rightarrow\widehat{SCA}=\left(SC;\left(ABCD\right)\right)\)
\(AC=\sqrt{AD^2+DC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\\AB\perp AD\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SAD\right)\)
\(\Rightarrow\left(AH;\left(SAD\right)\right)=90^0-\left(AH;AB\right)=90^0-\widehat{HAB}\)
Gọi E là trung điểm AB \(\Rightarrow ADCE\) là hình vuông \(\Rightarrow\widehat{ACE}=45^0\)
Tam giác BCE vuông cân tại E (do \(EB=EC=a\)) nên \(\widehat{ECB}=45^0\)
\(\Rightarrow\widehat{ACB}=90^0\) hay \(BC\perp AC\Rightarrow BC\perp\left(SAC\right)\) (do \(SA\perp BC\))
\(\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH\perp BH\)
Hay tam giác ABH vuông tại H
\(AH=\dfrac{SA.AC}{\sqrt{SA^2+AC^2}}=a\)
\(\Rightarrow cos\widehat{HAB}=\dfrac{AH}{AB}=\dfrac{1}{2}\Rightarrow\widehat{HAB}=60^0\)
\(\Rightarrow\widehat{HAB}=60^0\Rightarrow\left(AH;\left(SAD\right)\right)=30^0\)
Theo cmt \(BC\perp\left(SAC\right)\Rightarrow\left(SB;\left(SAC\right)\right)=\widehat{BSC}\)
\(SC=\sqrt{SA^2+AC^2}=2a\) ; \(SB=\sqrt{SA^2+AB^2}=a\sqrt{6}\)
\(\Rightarrow cos\widehat{BSC}=\dfrac{SC}{SB}=\dfrac{\sqrt{6}}{3}\Rightarrow\widehat{BSC}\approx35^016'\)
Câu 1: Cho hình vuông ABCD . Khẳng định sai là:
A. Hình vuông ABCD có bốn cạnh bằng nhau : AB = BC = CD = DA .
B. Hình vuông ABCD có bốn góc ở đỉnh: A,B,C,D bằng nhau.
C. Hình vuông ABCD có hai đường chéo bằng nhau: AC = BD .
D. Hình vuông ABCD có hai cặp cạnh đối song song: AB và BC ; CD và DA .
Câu 2: Một hình vuông có diện tích là 144 cm2 . Độ dài cạnh của hình vuông là:
A. 10 cm B. 12 cm C. 36 cm D. 24 cm
Câu 3: Hình vuông ABCD có chu vi là 20 cm . Diện tích của hình vuông ABCD là:
A. 100 cm2 B. 16 cm2 C. 36 cm2 D. 25 cm2
Câu 4: Một căn phòng hình vuông có diện tích 16 m2 được lát nền bởi các viên gạch loại 50 x 50 cm . Số gạch tối thiểu để lát nền căn phòng là:
A. 8 viên gạch. B. 16 viên gạch. C. 32 viên gạch. D. 64 viên gạch.
Câu 5: Số tự nhiên x là bội của 4 và thỏa mãn 24<x<30 . Số x là:
A. 28. B. 26. C. 24. D. 27.
Câu 6: Một đội y tế có 24 bác sĩ và 108 y tá. Có thể chia đội y tế đó nhiều nhất thành mấy tổ để các bác sĩ cũng như các y tá được chia đều vào mỗi tổ (số lượng bác sĩ và y tá của mỗi tổ là như nhau)?
A. 12. B. 6. C. 24. D. 18.
Câu 7: Một căn phòng hình chữ nhật có chiều dài là 680 cm và chiều rộng là 480 cm . Người ta muốn lát kín căn phòng đó bằng gạch hình vuông mà không có viên gạch nào bị cắt xén. Độ dài cạnh viên gạch lớn nhất có thể lát là:
A. 30 cm B. 20 cm C. 40 cm D. 60 cm
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA = 2 a và SA vuông góc với (ABCD). Góc giữa SC và ABCD bằng
A. 45 °
B. 30 °
C. 60 °
D. 90 °
Chọn A.
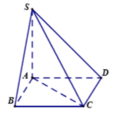
Vì SA vuông góc với đáy nên góc (SC,(ABCD)) = SCA.
Trong hình vuông ABCD có: AC = a 2 theo giả thiết, SA = a 2 => tam giác SAC vuông cân tại A
=> góc SCA = 45 °
Cho hình vuông ABCD biết diện tích hình vuông có cạnh gấp đôi hình vuông ABCD là 144 m2. Hỏi hình vuông có cạnh gấp 3 lần hình ABCD có diện tích bao nhiêu m2 ?
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A,B với AB=BC=a , AD=2a , SA vuông góc (ABCD) và SA = a√2 a) Cminh các mặt bên của hình chóp là các tam giác vuông
Cho hình chóp SABCD có SA vuông góc với (ABCD), SA=a\(\sqrt{2}\), đáy abcd là hình thang vuông tại A và D với AB=2a, AD=DC=a. Tính góc giữa (SBC) và (ABCD)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a. SO vuông góc (ABCD) và \(SO=\dfrac{a\sqrt{3}}{2}\). Tính \(\widehat{\left(SBC\right);\left(ABCD\right)}\)
Gọi E là trung điểm BC \(\Rightarrow OE\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}OE=\dfrac{1}{2}AB=\dfrac{a}{2}\\OE||AB\Rightarrow OE\perp BC\end{matrix}\right.\)
\(SO\perp\left(ABCD\right)\Rightarrow SO\perp BC\)
\(\Rightarrow BC\perp\left(SEO\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SEO}\) là góc giữa (SBC) và (ABCD)
\(tan\widehat{SEO}=\dfrac{SO}{OE}=\sqrt{3}\Rightarrow\widehat{SEO}=60^0\)
Cho hình vuông ABCD biết diện tích hình vuông có cạnh gấp 2 lần cạnh hình vuông ABCD là 144 m2 hỏi hình vuông có cạnh gấp 3 lần cạnh hình vuông ABCD có diện tích là bao nhiêu m2 ?
144 = 12 x 12
Vậy cạnh hình vuông có diện tích gấp 2 lần cạnh hình vuông ABCD là: 12m
Cạnh hình vuông ABCD là 12 : 2 = 6 m
Cạnh hình vuông cần tính là 6 x 3 = 18 m
Diện tích hình vuông đó là: 18 x 18 = 324 m2
Kí hiệu : Hình vuông có cạnh gấp 2 lần cạnh hình vuông ABCD là DEFG.
Hình vuông có cạnh gấp 3 lần cạnh hình vuông ABCD là MNPQ.
Giải.
Cạnh của hình vuông DEFG là 12cm (vì 12 x 12 = 144 cm2)
Cạnh của hình vuông ABCD là :
12 : 2 = 6(cm)
Cạnh của hình vuông MNPQ là :
6 x 3 = 18(cm)
Diệ tích hình vuông MNPQ là :
18 x 18 = 324 (cm2)
Đáp số : ...
Vì diện tích là 144m2 nên cạnh sẽ là 12 m vì 12*12=144(m2)
Cạnh hình vuông có thể là :
12:6*3=18(m)
Diện tích hình vuông là:
18*18=324(m2)
Đáp số:324m2