Giá trị nhỏ nhất của hàm số y = sin2 x- 4sinx – 5 là
A. – 20
B. – 8
C.0
D.9
Những câu hỏi liên quan
28 tháng 10 2023 lúc 12:30
Tìm giá trị lớn nhất của hàm số \(y=f\left(x\right)=sin^2x+4sinx-5\) trên \(\left[0;\dfrac{\pi}{2}\right]\)
A. \(-5\)
B. \(5\)
C. \(1\)
D. \(0\)
\(f'\left(x\right)=\left(sin^2x\right)'+4\cdot\left(sinx'\right)-5'\)
\(=2\cdot sinx\cdot cosx+4\cdot cosx=2cosx\left(sinx+2\right)\)
\(f'\left(x\right)=0\)
=>\(cosx\left(sinx+2\right)=0\)
=>\(cosx=0\)
=>\(x=\dfrac{\Omega}{2}+k\Omega\)
mà \(x\in\left[0;\dfrac{\Omega}{2}\right]\)
nên \(x=\dfrac{\Omega}{2}\)
\(f\left(\dfrac{\Omega}{2}\right)=sin^2\left(\dfrac{\Omega}{2}\right)+4\cdot sin\left(\dfrac{\Omega}{2}\right)-5\)
=1+4-5=0
\(f\left(0\right)=sin^20+4\cdot sin0-5=-5\)
=>Chọn D
Đúng 0
Bình luận (1)
Giá trị nhỏ nhất của hàm số
y
2
cos
2
x
+
4
sin
x
trên đoạn
0
;
π
2
là: A.
m
i
n
0
;
π
2...
Đọc tiếp
Giá trị nhỏ nhất của hàm số y = 2 cos 2 x + 4 sin x trên đoạn 0 ; π 2 là:
A. m i n 0 ; π 2 y = 4 - 2
B. m i n 0 ; π 2 y = 2 2
C. m i n 0 ; π 2 y = 2
D. m i n 0 ; π 2 y = 0
Chọn C.
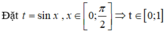
Khi đó, bài toán trở thành tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
trên đoạn [0;1]
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của hàm số
y
2
cos
2
x
+
4
sin
x
trên đoạn
0
;
π
2
A.
m
i
n
0
;
π
2
y
4
-...
Đọc tiếp
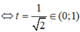
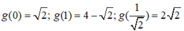
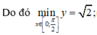
Tìm giá trị nhỏ nhất của hàm số y = 2 cos 2 x + 4 sin x trên đoạn 0 ; π 2
A. m i n 0 ; π 2 y = 4 - 2
B. m i n 0 ; π 2 y = 2 2
C. m i n 0 ; π 2 y = 2
D. m i n 0 ; π 2 y = 0
Giá trị nhỏ nhất của hàm số y = 3 cos 2 x - 4 sin x là:
A. 1
B. -7
C. -5
D. 11 3
Giá trị nhỏ nhất của hàm số y = 3 cos 2 x - 4 sin x là:
A. 1
B. -7
C. -5
D. 11 3
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y sin2 x + 3sin2x + 3cos2x
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = sin2 x + 3sin2x + 3cos2x
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số
y
4
sin
x
+
3
-
1
lần lượt là A.
2
v
à
2
. B.2 và 4 C.
4
2
v
à
8
. D.
4
2...
Đọc tiếp
Giá trị nhỏ nhất và giá trị lớn nhất của hàm số y = 4 sin x + 3 - 1 lần lượt là
A. 2 v à 2 .
B.2 và 4
C. 4 2 v à 8 .
D. 4 2 - 1 v à 7 .
Do đó giá trị nhỏ nhất và giá trị nhỏ nhất của hàm số đã cho là 4 2 - 1 và 7
Đáp án D
Đúng 0
Bình luận (0)
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số y
4
sin
x
+
π
2
+
cos
x
+
π
2
+
3
2
-
1
là:
Đọc tiếp
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y = 4 sin x + π 2 + cos x + π 2 + 3 2 - 1 là:
Hàm số
y
4
sin
x
−
3
cos
x
có giá trị lớn nhất M, giá trị nhỏ nhất m là A.
M
7
,
m
1
B.
M
5
,
m
−
5
C.
M
1
,
m
−
7
D.
M...
Đọc tiếp
Hàm số y = 4 sin x − 3 cos x có giá trị lớn nhất M, giá trị nhỏ nhất m là
A. M = 7 , m = 1
B. M = 5 , m = − 5
C. M = 1 , m = − 7
D. M = 7 , m = − 7
Đáp án B
Ta có y = 4 sin x − 3 cos x = 5 4 5 sinx − 3 5 cos x = 5 sin x − α với sin α = 3 5 cos α = 4 5
Ta có − 1 ≤ sin x − α ≤ 1 ⇒ − 5 ≤ 5 sin x − α ≤ 5 ⇒ M = 5 m = − 5
Đúng 0
Bình luận (0)