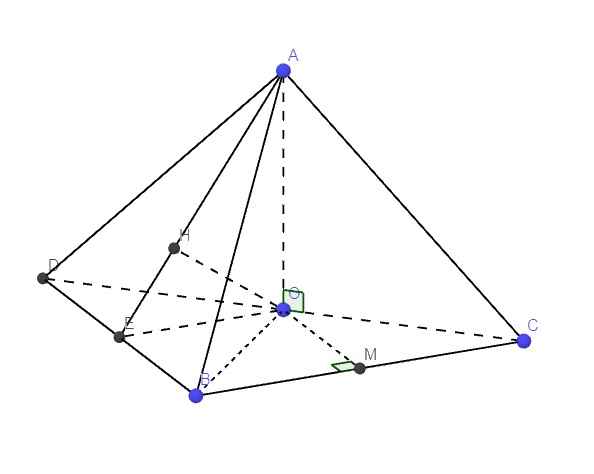
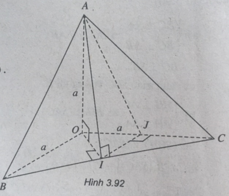
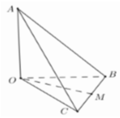
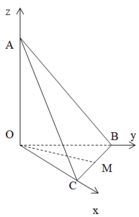
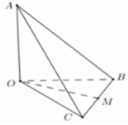
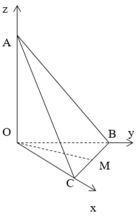
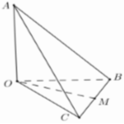
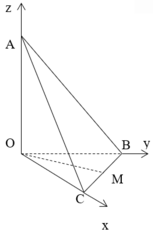
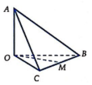
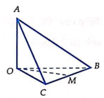
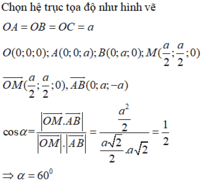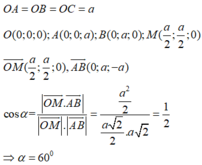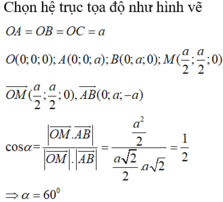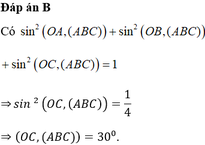Xét tứ diện O.ABC có OA, OB, OC đôi một vuông góc. Gọi α , β , γ lần lượt là góc giữa các đường thẳng OA, OB, OC với mặt phẳng (ABC). Khi đó, tính giá trị nhỏ nhất của biểu thức sau M= (3+ c o t 2 α )(3+ c o t 2 β )(3+ c o t 2 γ )
A. Số khác
B. 48 3
C. 48
D. 125





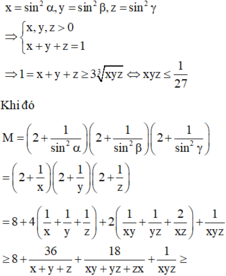
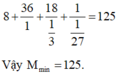

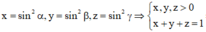
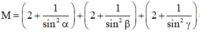
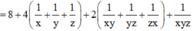
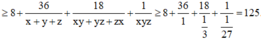 .
.