Đáp án D
Gọi H là hình chiếu của O lên (ABC) ⇒ H là trực tâm ∆ A B C .
Ta có O A ; A B C ^ = O A ; A H ^ = O A H ^ = α tương tự O B H ^ = β , O C H ^ = γ
Lại có
![]()
![]()
Đặt
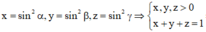
![]()
Khi đó
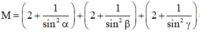
![]()
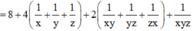
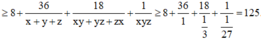 .
.
Vậy M m i n = 125 .
Đáp án D
Gọi H là hình chiếu của O lên (ABC) ⇒ H là trực tâm ∆ A B C .
Ta có O A ; A B C ^ = O A ; A H ^ = O A H ^ = α tương tự O B H ^ = β , O C H ^ = γ
Lại có
![]()
![]()
Đặt
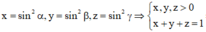
![]()
Khi đó
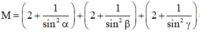
![]()
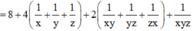
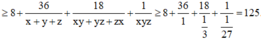 .
.
Vậy M m i n = 125 .
Xét tứ diện O.ABC có OA, OB, OC đôi một vuông góc. Gọi α , β , γ lần lượt là góc giữa các đường thẳng OA, OB, OC với mặt phẳng (ABC). Khi đó, tính giá trị nhỏ nhất của biểu thức sau M = 3 + c o t 2 α 3 + c o t 2 β 3 + c o t 2 γ
A. Số khác
B. 48 3
C. 48
D. 125
Cho tứ diện OABC có OA,OB,OC đôi một vuông góc. Góc giữa mặt phẳng (ABC) và các đường thẳng OA,OB lần lượt là 30 ° và 45 ° . Tính góc giữa đường thẳng OC và mặt phẳng (ABC).
A. 45 °
B. 30 °
C. 60 °
D. 90 °
Tứ diện OABC có OA,OB,OC đôi một vuông góc và O A = 1 , O B = 2 , O C = 3 . Tang của góc giữa đường thẳng OA và mặt phẳng (ABC) bằng
A. 6 7
B. 14 6
C. 6 13 13
D. 6 7 7
Tứ diện OABC có OA, OB, OC đôi một vuông góc và O A = 1 , O B = 2 , O C = 3 . Tan của góc giữa đường thẳng OA và mặt phẳng A B C bằng
A. 13 6
B. 6 7
C. 6 7 7
D. 6 13 13
Tứ diện OABC có OA,OB,OC đôi một vuông góc và OA=1,OB=2,OC=3. Tang của góc giữa đường thẳng OA và mặt phẳng (ABC) bằng
A. 6 7
B. 13 6
C. 6 13 13
D. 6 7 7
Cho tứ diện OABC biết OA, OB, OC đôi một vuông góc với nhau, biết O A = 3 , O B = 4 và thể tích khối tứ diện OABC bằng 6. Khi đó khoảng cách từ O đến mặt phẳng (ABC) bằng:
A. 3
B. 41 12
C. 144 41
D. 12 41
Cho tứ diện OABC có ba cạnh OA;OB;OC đôi một vuông góc với nhau, O A = a 2 2 , O B = O C = a . Gọi H là hình chiếu của điểm O trên mặt phẳng (ABC)Tính thể tích khối tứ diện OABH
A. a 3 2 6
B. a 3 2 12
C. a 3 2 24
D. a 3 2 48
Cho tứ diện OABC có OA,OB,OC đội một vuông góc, O A = a , O B = b , O C = c . Tính khoảng cách d từ O tới mặt phẳng (ABC).
A. d = a b c a 2 b 2 + b 2 c 2 + c 2 a 2
B. d = a 2 + b 2 + c 2 3
C. d = a b + b c + c a a 2 + b 2 + c 2
D. d = a 2 b 2 c 2 a 2 b 2 + b 2 c 2 + c 2 a 2
Cho tứ diện OABC có OA,OB,OC đôi một tạo với nhau góc và OA=OB=a,OC=2a. Côsin góc giữa đường thẳng OC và mặt phẳng (ABC) bằng
A. 5 3
B. 1 3
C. 2 3
D. 2 3 3