Tìm các điểm cực trị của hàm số y = x 3 5 ( 4 - x ) , x>0.
A. x=2
B. x = 3 2
C. x=6
D. x=4
Cho hàm số y = x 3 - 2 x 2 - 1 (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0
B. 1
C. 2
D. 3
Chọn D
Ta có: y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;
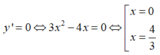
y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3
Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
1,Tìm tất cả các giá trị của m để hàm số y=2x^2 - 3mx + m - 2 trên x-1 đạt cực đại tại điểm x=2. 2, Tìm tất cả các giá trị của m để hàm số y= x^2 + mx +1 trên x+m đạt cực tiểu tại điểm x=2. 3, Tìm tất cả các giá trị của m để hàm số y=x^2 -(2m-1)x+3 trên x+2 có cực đại và cực tiểu . 4, Tìm m để hso y=x^2 +m(m^2-1)x-m^4+1 trên x-m có cực đại và cực tiểu. Mọi người giúp em với ạ . Em cảm ơn ạ !
Tìm các điểm cực trị và các giá trị cực trị của hàm số \(y = \sqrt{2x-x^3}\)
ĐKXĐ: \(2x-x^3>=0\)
=>\(x^3-2x< =0\)
=>\(\left[{}\begin{matrix}x< =-\sqrt{2}\\0< =x< =\sqrt{2}\end{matrix}\right.\)
\(y=\sqrt{2x-x^3}\)
=>\(y'=\dfrac{\left(2x-x^3\right)'}{2\cdot\sqrt{2x-x^3}}=\dfrac{2-3x^2}{2\cdot\sqrt{2x-x^3}}\)
Đặt y'=0
=>\(2-3x^2=0\)
=>\(3x^2=2\)
=>\(x^2=\dfrac{2}{3}\)
=>\(\left[{}\begin{matrix}x=\dfrac{\sqrt{6}}{3}\left(nhận\right)\\x=-\dfrac{\sqrt{6}}{3}\left(loại\right)\end{matrix}\right.\)
Khi \(x=\dfrac{\sqrt{6}}{3}\) thì \(y=\sqrt{2\cdot\dfrac{\sqrt{6}}{3}-\left(\dfrac{\sqrt{6}}{3}\right)^3}\)
\(=\sqrt{\dfrac{4\sqrt{6}}{9}}=\dfrac{2}{3}\cdot\sqrt{\sqrt{6}}\)
Tìm các điểm cực trị của hàm số y = x 4 5 ( x - 4 ) 2 , x>0.
A. x=4 và x=8/7.
B. x=4.
C. x=2.
D. x=2 và x = 4/9.
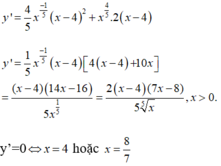
Ta thấy y’ đổi dấu khi đi qua 2 điểm x=4 và x = 8/7 nên đây là 2 điểm cực trị của các hàm số đã cho.
Chọn đáp án A.
Tìm tập hợp tất cả các giá trị thực của tham số m để hàm số y = | x | 3 - ( 2 m + 1 ) x 2 + 3 m | x | - 5 có 3 điểm cực trị.
A. - ∞ ; 1 4
B. 1 ; + ∞
C. ( - ∞ ; 0 ]
D. 0 ; 1 4 ∪ 1 ; + ∞
Cho hàm số y = 1 3 x 3 - ( m + 1 ) x 2 + ( m + 3 ) x + m - 4 . Tìm m để hàm số y=f(|x|) có 5 điểm cực trị
A. -3<m<-1
B. m>1
C. m>4
D. m>0
Cho hàm số ![]() . Tìm tất cả các giá trị của tham số m để hàm số
y
=
f
(
x
)
có 5 điểm cực trị.
. Tìm tất cả các giá trị của tham số m để hàm số
y
=
f
(
x
)
có 5 điểm cực trị.
![]()
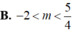
![]()
![]()
tìm m để đồ thị hàm số \(y=x^4+2\left(m-2\right)x^2+m^2-5m+5\) có 3 điểm cực trị là các đỉnh của một tam giác đều
\(y'=4x^3+4\left(m-2\right)x=0\Rightarrow\left[{}\begin{matrix}x=0\\x^2=2-m\end{matrix}\right.\)
Hàm có 3 cực trị khi và chỉ khi \(2-m>0\Leftrightarrow m< 2\)
Khi đó gọi 3 cực trị là A, B, C ta có: \(\left\{{}\begin{matrix}A\left(0;m^2-5m+5\right)\\B\left(\sqrt{2-m};1-m\right)\\C\left(-\sqrt{2-m};1-m\right)\end{matrix}\right.\)
Tam giác ABC luôn cân tại A
Gọi H là trung điểm BC \(\Rightarrow H\left(0;1-m\right)\)
\(AH=\left|y_A-y_H\right|=\left|m^2-4m+4\right|=\left(m-2\right)^2\)
\(BC=2\sqrt{2-m}\)
Do ABC đều \(\Rightarrow AH=\dfrac{\sqrt{3}}{2}BC\Leftrightarrow\left(m-2\right)^2=\dfrac{\sqrt{3}}{2}\sqrt{2-m}\)
\(\Leftrightarrow\left(2-m\right)^3=\dfrac{3}{4}\Rightarrow m=2-\sqrt[3]{\dfrac{3}{4}}\)