Điểm cực tiểu của hàm số y = x 4 + 4 x 2 + 2 là:
A. x = 1
B. x = 2
C. x = 0
D. Không tồn tại
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ ( a ; b ) . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' ( x 0 ) = 0 .
(2) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = f ' ' ( x 0 ) = 0 thì điểm x 0 không phải là điểm cực trị của hàm số y = f ( x ) .
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
(4) Nếu hàm số y = f ( x ) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' ( x 0 ) = 0 , f ' ' ( x 0 ) > 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f ( x ) .
A. 1
B. 2
C. 0
D. 3
Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng
\(y=x^4-2\left(m^2-m+1\right)x+m-1\)
\(y'=4x^3-4\left(m^2-m+1\right)x\)
\(y'=0\Leftrightarrow4x^3-4\left(m^2-m+1\right)x=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=\pm\sqrt{m^2-m+1}\end{cases}}\)
Khoảng cách giữa hai điểm cực tiểu là:
\(2\sqrt{m^2-m+1}=2\sqrt{\left(m-\frac{1}{2}\right)^2+\frac{3}{4}}\ge2\sqrt{\frac{3}{4}}\)
Dấu \(=\)khi \(m-\frac{1}{2}=0\Leftrightarrow m=\frac{1}{2}\).
Cho hàm số f có đạo hàm f ' ( x ) = x ( x + 1 ) 2 ( x - 1 ) 4 , số điểm cực tiểu của hàm số f là bao nhiêu?
A. 3
B. 2
C. 0
D. 1
Đáp án là D.
• Ta có: f , ( x ) = x ( x + 1 ) 2 ( x - 1 ) 4 = 0 ⇔ x = 0 x = ± 1
• Bảng biến thiên:
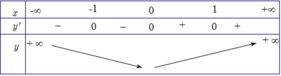
Câu 3 Để đồ thị hàm số \(y=-x^4-\left(m-3\right)x^2+m+1\) có điểm cực đạt mà không có điểm cực tiểu thì tất cả giá trị thực của tham số m là
Câu 4 Cho hàm số \(y=x^4-2mx^2+m\) .Tìm tất cả các giá trị thực của m để hàm số có 3 cực trị
Hoành độ các điểm cực tiểu của hàm số y = x 4 + 3 x 2 + 2 là:
A. x = −1; B. x = 5;
C. x = 0; D. x = 1, x = 2.
Đáp án: C
Ta có y(0) = 2, y(a) = a 4 + 3a x 2 + 2 > 2 với mọi a ≠ 0.
Vậy hàm số có một điểm cực tiểu là x = 0.
Hoành độ các điểm cực tiểu của hàm số y = x 4 + 3 x 2 + 2 là:
A. x = −1; B. x = 5;
C. x = 0; D. x = 1, x = 2.
Đáp án: C
Ta có y(0) = 2, y(a) = a 4 + 3a x 2 + 2 > 2 với mọi a ≠ 0.
Vậy hàm số có một điểm cực tiểu là x = 0.
Cho hàm số liên tục trên khoảng (a;b) và x 0 ∈ a ; b . Có bao nhiêu mệnh đề đúng trong các mệnh đề sau ?
(1) Hàm số đạt cực trị tại điểm x 0 khi và chỉ khi f ' x 0 = 0
(2) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = f " x 0 = 0 thì điểm x 0 không là điểm cực trị của hàm số y = f x
(3) Nếu f'(x) đổi dấu khi x qua điểm x 0 thì điểm x 0 là điểm cực tiểu của hàm số y = f(x)
(4) Nếu hàm số y = f(x) có đạo hàm và có đạo hàm cấp hai tại điểm x 0 thỏa mãn điều kiện f ' x 0 = 0 , f " x 0 > 0 thì điểm x 0 là điểm cực đại của hàm số y = f(x)
A. 1
B. 2
C. 0
D. 3
Cho hàm số y = f(x) có đồ thị của hàm số y = f '(x) được cho như hình bên và các mệnh đề sau: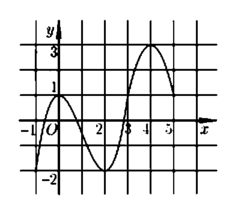
(1). Hàm số y = f(x) đồng biến trên khoảng (-1;0)
(2). Hàm số y = f(x) nghịch biến trên khoảng (1;2)
(3). Hàm số y = f(x) đồng biến trên khoảng (3;5)
(4). Hàm số y = f(x) có hai điểm cực đại và một điểm cực tiểu.
Số mệnh đề đúng là
A. 1
B. 3
C. 4
D. 2
Đáp án D
Dựa vào hình vẽ, ta thấy rằng
+ Đồ thị hàm số f '(x) cắt Ox tại 3 điểm phân biệt x 1 - 1 ; 0 , x 2 0 ; 1 , x 3 2 ; 3
Và f '(x) đổi dấu từ - → + khi đi qua x 1 , x 3 ⇒ Hàm số có 2 điểm cực tiểu, 1 điểm cực đại
+ Hàm số y = f(x) nghịch biến trên khoảng - 1 ; x 1 đồng biến trên x 1 ; x 2 (1) sai
+ Hàm số y = f(x) nghịch biến trên khoảng x 2 ; x 3 (chứa khoảng (1;2)), đồng biến trên khoảng x 3 ; 5 (chứa khoảng (3;5)) ⇒ 2 ; 3 đúng
Vậy mệnh đề 2,3 đúng và 1, 4 sai.
Cho hàm số y= mx^2 +2(m^2-5)x^4 +4 . Có bao nhiêu số nguyên m để hàm số có 3 điểm cực trị trong đó có đúng 2 điểm cực đại và 1 điểm cực tiểu.
Đề đúng là \(y=mx^2+2\left(m^2-5\right)x^4+4\) chứ bạn (nghĩa là ko bị nhầm lẫn vị trí \(x^2\) và \(x^4\))
Hàm có đúng 2 điểm cực đại và 1 điểm cực tiểu khi:
\(\left\{{}\begin{matrix}2\left(m^2-5\right)< 0\\2\left(m^2-5\right).m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \sqrt{5}\)
\(\Rightarrow\) có 2 giá trị nguyên của m thỏa mãn
Cho hàm số y = x 3 - 2 x 2 - 1 (1) và các mệnh đề
(1) Điểm cực trị của hàm số (1) là x = 0 hoặc x = 4/3
(2) Điểm cực trị của hàm số (1) là x = 0 và x = 4/3
(3) Điểm cực trị của đồ thị hàm số (1) là x = 0 và x = 4/3
(4) Cực trị của hàm số (1) là x = 0 và x = 4/3
Trong các mệnh đề trên, số mệnh đề sai là:
A. 0
B. 1
C. 2
D. 3
Chọn D
Ta có: y ' = 3 x 2 - 4 x , y ' ' = 6 x - 4 ;
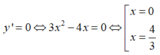
y''(0) = -4 < 0; y''(4/3) = 4 > 0. Do đó hàm số có hai cực trị là x = 0 và x = 4/3
Các mệnh đề (1); (2) và (3) sai;mệnh đề (4) đúng.