Tính tích phân sau: I = ∫ 2 10 d x x - 2 x - 1
A. 1 + 2 ln 2
B. 2 9 + 2 ln 9 5
C. 2 ln 9 5 - 2 9
D. 2 ln 2 - 1
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho (P) : y= \(x^2-4x+3\)và đường thẳng (d): y= m(x-2)-1. Tính tổng các giá trị của tham số m để đường thẳng (d) cắt (P) tại 2 điểm phân biệt A, B sao cho diện tích tam giác IAB bằng 10 với điểm I(2;3).
Cho hàm số f(x) thỏa mãn ∫ 0 1 ( x + 1 ) f ' ( x ) d x = 10 và 2f(1) - f(0) = 2 .Tính tích phân I = ∫ 0 1 f ( x ) d x .
A. I=-12.
B. I=8.
C. I=12.
D. I=-8
Phân tích các đa thức sau thành nhân tử:
a) (x^3)-3(x^2)+1-3x b) 3(x^2)-6xy+3(y^2)-12(z^2) c) (x^2)-7xy+10(y^2) d) (x+1)(x+2)(x+3)(x+4)-8
Tính tích phân sau :
\(I=\int\frac{2dx}{2\sin x-\cos x+1}\)
Đặt \(t=\tan\frac{x}{2}\rightarrow dx=\frac{2dt}{1+t^2}\)
Khi đó : \(I=\int\frac{4\frac{dt}{1+t^2}}{\frac{4}{1+t^2}-\frac{1-t^2}{1+t^2}+1}=\int\frac{2dt}{1+2t^2}=\int\left(\frac{1}{t}-\frac{1}{t+2}\right)dt=\ln\left|\frac{1}{t+2}\right|+C=\ln\left|\frac{\tan\frac{x}{2}}{\tan\frac{x}{2}+2}\right|+C\)
Phân tích các đa thức sau thành nhân tử:
a) (x-2)(x+2)(x^2 - 10) -72
b) x^8 + x^6 + x^4 + x^2 + 1
c) (x +y)^4 + x^4 + y^4
d) (x+1)^4 + (x^2 + x + 1)^2
a) (x-2)(x+2)(x^2-10)-72=(x^2-4)(x^2-82)
b) x^8+x^6+x^4+x^2+1=x^2 (x^4+x^3+x^2+1+1/x^2)
c)(x+y)^4+x^4+y^4=(x+y)^4+(x+y)^4=2 (x+y)^4
a) (x-2)(x+2)(x^2 - 10) -72
= (x^2 - 4)(x^2 - 10) - 72
= x^4 - 4x^2 -10x^2 + 40 - 72
= x^4 - 14x^2 - 32
= x^4 - 16x^2 + 2x^2 - 32
= x^2(x^2 - 16) + 2(x^2 - 16)
= (x^2 - 16)(x^2 + 2)
= (x-4)(x+4)(x^2 + 2)
c) (x+y)4 + x4 + y4
= 2x4 + 4xy3 + 6x2y2 + 4x3y + 2y3
= 2(y4 + 2xy3 + 3x2y2 + 2x3y + x4)
= 2(y2 + xy + y2)2
\(d,(x+1)^4+(x^2+x+1)^2\)
\(=x^4+4x^3+6x^2+4x+1+x^4+2x^3+3x^2+2x+1\)
\(=(x^4+x^4)+(4x^3+2x^3)+(6x^2+3x^2)+(4x+2x)+(1+1)\)
\(=2x^4+6x^3+9x^2+6x+2\)
\(=\left[x^2+2x+2\right]\left[2x^2+2x+1\right]\)
Cho tích phân I = ∫ 0 2 f ( x ) d x = 2 . Tính tích phân J = ∫ 0 2 3 f ( x ) - 2 d x
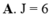
![]()
![]()
![]()
* Phân tích các đa thức sau thành nhân tử:
A= x2 + 13x - 30
B= -x2 + 3x - 2
* Tính:
a) 4x2 - 169
b) 121x3 - 27
c) (x + 10)3
d) x3 + y3
Bài 1
A= x2 + 13x - 30 = x2 + 15x - 2x - 30 = ( x2 +15x) - ( 2x+30) = x(x+15) - 2(x+15) = (x+15)(x-2)
B = -x2+3x-2 = -(x2 - 3x +2 )= -( x2 - x - 2x +2) = - [(x2 - x) - ( 2x - 2)] = - [x(x - 1) - 2(x - 1)] = (x - 1)(x - 2)
Bài 2
a) 4x2 - 169 = (2x)2 - 132 = ( 2x - 13)(2x + 13)
b) 121x3 - 27 đề sai hay sao ý
c) (x + 10)3 = x3 + 30x2 + 300x + 100
d) x3 + y3 = (x + y)(x2 - xy - y2)
k cho mình nhé bạn. Thanks you ! ^^
\(x^2+13x-30\)
\(=x^2+2x-15x-30\)
\(=x\left(x+2\right)-15\left(x+2\right)\)
\(=\left(x+2\right)\left(x-15\right)\)
Phân tích các đa thức sau thành nhân tử (tách một hạng tử thành nhiều hạng tử)
f) x^2-5x-14
i) x^2-7x+10
h) x^2-7x+12
g) x^2+6x+5
f)\(x^2-5x-14=x^2-7x+2x-14=x\left(x-7\right)+2\left(x-7\right)=\left(x-7\right)\left(x+2\right)\)
i)\(x^2-7x+10=x^2-2x-5x+10=x\left(x-2\right)-5\left(x-2\right)=\left(x-5\right)\left(x-2\right)\)
h)\(x^2-7x+12=x^2-3x-4x+12=x\left(x-3\right)-4\left(x-3\right)=\left(x-4\right)\left(x-3\right)\)
g)\(x^2+6x+5=x^2+x+5x+5=x\left(x+1\right)+5\left(x+1\right)=\left(x+1\right)\left(x+5\right)\)
f)\(x^2-5x-14=x^2-7x+2x-14\)
\(=\left(x+2\right)\left(x-7\right)\)
i)\(x^2-7x+10=x^2-5x-2x+10\)
\(=\left(x-2\right)\left(x-5\right)\)
h)\(x^2-7x+12=x^2-4x-3x+12\)
\(=\left(x-3\right)\left(x-4\right)\)
g)\(x^2+6x+5=x^2+x+5x+5\)
\(=\left(x+5\right)\left(x+1\right)\)
f) \(x^2-5x-14\)
\(=x^2-7x+2x-14\)
\(=\left(x^2-7x\right)+\left(2x-14\right)\)
\(=x\left(x-7\right)+2\left(x-7\right)\)
\(=\left(x+2\right)\left(x-7\right)\)
i) \(x^2-7x+10\)
\(=x^2-5x-2x+10\)
\(=\left(x^2-5x\right)-\left(2x-10\right)\)
\(=x\left(x-5\right)-2\left(x-5\right)\)
\(=\left(x-2\right)\left(x-5\right)\)
h) \(x^2-7x+12\)
\(=x^2-3x-4x+12\)
\(=\left(x^2-3x\right)-\left(4x-12\right)\)
\(=x\left(x-3\right)-4\left(x-3\right)\)
\(=\left(x-4\right)\left(x-3\right)\)
g) \(x^2+6x+5\)
\(=x^2+x+5x+5\)
\(=\left(x^2+x\right)+\left(5x+5\right)\)
\(=x\left(x+1\right)+5\left(x+1\right)\)
\(=\left(x+5\right)\left(x+1\right)\)
Phân tích các đa thức sau thành nhân tử
a) x^2+2xy-9+y^2
b) 5x^2 - 10xy + 5y^2 -20z^2
c) x^2 - 7x + 10
d) 2x^2 + 7x +6
a) (x^2+2xy+y^2)-9=(x+y)^2-9=(x+y-3)(x+y+3)
b) 5(x^2-2xy+y^2-4z^2)=5[(x-y)^2-4z^2]=5[(x-y-2z)(x-y+2z)
c)x^2-2x-5x+10=x(x-2)-5(x-2)=(x-5)(x-2)
d)2x^2-4x-3x+6=2x(x-2)-3(x-2)=(2x-3)(x-2)
Tính tích phân bất định hàm số hữu tỉ sau :
\(I=\int x^2\left(2-3x^2\right)^8dx\)
Đặt \(t=2-3x^2\)\(\Rightarrow\begin{cases}dt=-6xdx\\x^2=\frac{2-t}{3}\end{cases}\)\(\Leftrightarrow x^2\left(2-3x^2\right)^8=\left(\frac{2-t}{3}\right)t^8=\frac{1}{3}\left(2t^8-t^9\right)\)
Vậy :
\(I=\int x^2\left(2-3x^2\right)^8dx=\frac{1}{3}\left(2\int t^8dt-\int t^9dt\right)=\frac{2}{27}t^9-\frac{1}{30}t^{10}+C\)
\(=\frac{2}{27}\left(2-3x^2\right)^9-\frac{1}{30}\left(2-3x^2\right)^{10}+C\)