Cho f(x) liên tục trên 0 ; 5 thỏa mãn ∫ 0 5 f ( x ) d x = 5 , ∫ 1 3 f ( x ) d x = 1 , khi đó giá trị của P = ∫ 0 1 f ( x ) d x + ∫ 3 5 f ( x ) d x là:
A. 4
B. -4
C. Không tính được
D. 6
Cho các mệnh đề:
1. Nếu hàm số y=f(x) liên tục trên a ; b và f a . f b < 0 thì tồn tại x 0 ∈ a ; b sao cho f x 0 = 0.
2. Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm.
3. Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì phương trình f x = 0 có nghiệm duy nhất trên ( a ; b ) .
Trong ba mệnh đề trên
A. Có đúng hai mệnh đề sai
B. Cả ba mệnh đề đều đúng
C. Cả ba mệnh đề đều sai
D. Có đúng một mệnh đề sai
Đáp án D
Định lí: “Nếu hàm số y = f x liên tục trên a ; b và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho f c = 0 ”.
Mệnh đề 1: SAI ở giả thiết (a;b).
Mệnh đề 2: Nếu hàm số y=f(x) liên tục trên a ; b
và f a . f b < 0 thì tồn tại ít nhất một điểm c ∈ a ; b sao cho c hay f x = 0 là nghiệm của phương trình f(x)=0 nên mệnh đề 2 ĐÚNG.
Mệnh đề 3: Nếu hàm số y=f(x) liên tục, đơn điệu trên a ; b và f a . f b < 0 thì đồ thị hàm số y=f(x) cắt trục Ox tại duy nhất một điểm thuộc khoảng (a;b) nên f(x)=0 có nghiệm duy nhất trên (a;b). Do đó mệnh đề 3 ĐÚNG
cho f(x)=\(\dfrac{2x-1}{x^3-4}\), khẳng định đúng là?
a. f(x) liên tục trên (-2,2)
b. f(x) liên tục trên (-2,0)
c. f(x) liên tục tại x=2
d. f(x) liên tục tại x=0
help pls
Mình nghĩ là tìm khẳng định sai chứ, vì b,c,d đều đúng
\(DKXD:x\ne\sqrt[3]{4}\approx1,58\in\left(-2;2\right)\)
Vậy thì hàm sẽ gián đoạn trên khoảng \(\left(-2;2\right)\) => đáp án A sai, còn lại tất cả đều đúng
Cho f(x) là hàm số liên tục trên R thỏa mãn f(x) + f'(x) = x và f(0) = 1. Tính f(1).
A. 2/e
B. 1 / e
C. e
D. e / 2
Chọn A
![]() .
.
Nhân 2 vế của ![]() với
với ![]() ta được
ta được ![]() .
.
Hay ![]() .
.
Xét ![]() .
.
Đặt ![]() .
.
![]()
Suy ra ![]() .
.
Theo giả thiết ![]() nên
nên ![]()
![]() .
.
Cho hàm số f ( x ) = 3 - 9 - x x , 0 < x < 9 m , x = 0 3 x , x ≥ 9 . Tìm m để f(x) liên tục trên [ 0 ; + ∞ )
A. 1 3
B. 1 2
C. 1 6
D. 1
Cho hàm số f(x) liên tục trên [0;1]. Biết ∫ 0 1 x . f ' 1 - x - f x d x = 1 2 . Tính f(0).
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số f(x) liên tục trên có f(0) = 0 và đồ thị hàm số y = f’(x) như hình vẽ bên. Hàm số đồng biến trên khoảng
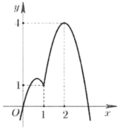
A. 2 ; + ∞
B. - ∞ ; 2
C. (0;2)
D. (1;3)
Cho hàm số f(x) liên tục trên tập R thỏa mãn f ' x x 2 + 1 = 2 x f x + 1 và f(x) > -1, f(0)=0. Tính f 3 .
A. ![]() .
.
B. 9.
C. 3.
D. 0.
Cho hàm số y = f(x) liên tục trên có bảng biến thiên như sau:

Biết f(0)<0, phương trình f(|x|)=f(0) có bao nhiêu nghiệm?
A. 4
B. 5
C. 3
D. 2
Đáp án C
Phương pháp: Từ BBT của đồ thị hàm số y = f(x) suy ra BBT của đồ thị hàm số y = f(|x|), số nghiệm của phương trình f(|x|) = 0 là số giao điểm của đồ thị hàm số y = f(|x|) và đường thẳng y = f(0)
Cách giải: Từ bảng biến thiên hàm số y = f(x) ta có bảng biến thiên hàm số f(|x|) = f(0) như sau:

Suy ra, phương trình f(|x|) = f(0) có 3 nghiệm
Cho hàm số y = f ( x ) liên tục trên 0 ; + ∞ .
Biết f ' ( x ) ln ( x ) x v à f ( 1 ) = 3 2 và tính f ( 3 )
![]()
![]()
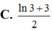
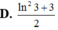
Cho hàm số f ( x ) = 3 - 9 - x x , 0 < x < 9 m , x = 0 3 x , x ≥ 9 Tìm m để f(x) liên tục trên [0; +∞) là.
A. 1/3.
B. 1/2.
C. 1/6.
D. 1.
Chọn C.
TXĐ: D = [0; +∞).
Với x = 0 ta có f(0) = m.
Ta có 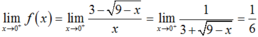 .
.
Vậy để hàm số liên tục trên [0; +∞) khi 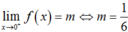 .
.