Chọn A
![]() .
.
Nhân 2 vế của ![]() với
với ![]() ta được
ta được ![]() .
.
Hay ![]() .
.
Xét ![]() .
.
Đặt ![]() .
.
![]()
Suy ra ![]() .
.
Theo giả thiết ![]() nên
nên ![]()
![]() .
.
Chọn A
![]() .
.
Nhân 2 vế của ![]() với
với ![]() ta được
ta được ![]() .
.
Hay ![]() .
.
Xét ![]() .
.
Đặt ![]() .
.
![]()
Suy ra ![]() .
.
Theo giả thiết ![]() nên
nên ![]()
![]() .
.
Cho hàm số y= f(x) có đạo hàm liên tục trên khoảng ![]() thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên đoạn [1;e] thỏa mãn f 1 = 1 2 và x . f ' x = xf 2 x - 3 f x + 1 x , ∀ x ∈ 1 ; e . Giá trị của f(e) bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y=f(x) thỏa mãn f ' ( x ) + 2 x f ( x ) = e - x 2 , ∀ x ∈ R và f(1)=0 Tính giá trị f(2).
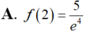
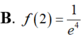
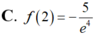
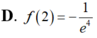
Cho hàm số y=f(x) liên tục trên R thỏa mãn ∫ f ( x ) d x = e - 2018 x + C . Khẳng định nào sau đây là đúng?
![]()
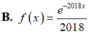
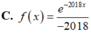
![]()
Cho hàm số y = f ( x ) liên tục trên R \ { - 1 ; 0 } thỏa mãn f ( 1 ) = 2 ln 2 + 1 , x ( x + 1 ) f ' ( x ) + ( x + 2 ) f ( x ) = x ( x + 1 ) , ∀ x ∈ R \ { - 1 ; 0 } Biết f ( 2 ) = a + b ln 3 với a, b là hai số hữu tỉ. Tính T = a 2 - b
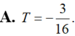
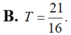
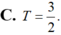
![]()
Cho hàm số f(x) liên tục trên tập R thỏa mãn f ' x x 2 + 1 = 2 x f x + 1 và f(x) > -1, f(0)=0. Tính f 3 .
A. ![]() .
.
B. 9.
C. 3.
D. 0.
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên R và thỏa mãn f ' ( x ) ∈ [ - 1 ; 1 ] với ∀ x ∈ ( 0 ; 2 ) Biết f(0) = f(2) = 1 Đặt I = ∫ 0 2 f ( x ) d x phát biểu dưới đây là ĐÚNG ?
![]()
![]()
![]()
![]()
Cho hàm số y = f(x) liên tục trên khoảng 0 ; + ∞ . Biết f(1) = 1 và f(x) = xf'(x) + ln (x). Giá trị f(e) bằng
A. e
B. 1
C. 2
D. 1 e