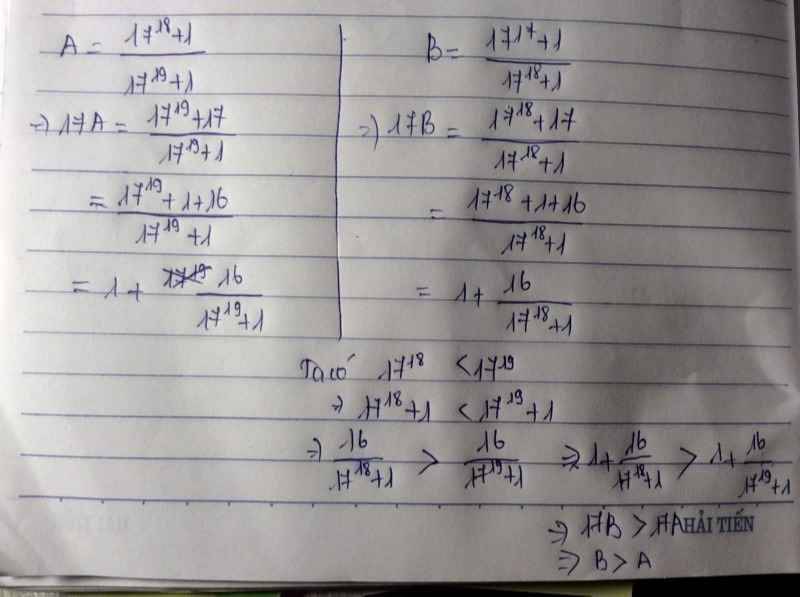Giải ra giúp tôi với mấy thánh

Xét tử:

tử = 1/18 + 2/17 + 3/16 + ... + 18/1 + (1+1+1+...+1)(18 số 1)

    =(1/18 + 1)+(2/17 + 1)+...+(18/1 + 1)

    =19/18 + 19/17 + ... + 19/1

    =19(1/18 + 1/17 + ... + 1/1)

Nên tử/ mẫu =19

Nếu nghĩ kĩ thì thấy bài này cũng đơn giản thôi.Thử xem cách giải của mk nè:

Giải: Ta có: A=\(\frac{17^{18}+1}{17^{19}+1}\)                                                        B=\(\frac{17^{17}+1}{17^{18}+1}\)

               17A=\(\frac{17^{19}+17}{17^{19}+1}\)                                                 17B=\(\frac{17^{18}+17}{17^{18}+1}\)

             17A=\(\frac{\left(17^{19}+1\right)+16}{17^{19}+1}\)                                       17B=\(\frac{\left(17^{18}+1\right)+16}{17^{18}+1}\)

               17A=\(\frac{17^{19}+1}{17^{19}+1}+\frac{16}{17^{19}+1}\)                             17B=\(\frac{17^{18}+1}{17^{18}+1}+\frac{16}{17^{18}+1}\)

               17A=\(1+\frac{16}{17^{19}+1}\)                                            17B= \(1+\frac{16}{17^{18}+1}\)

 Lại có: 17¹⁹+1>17¹⁸+1

 Suy ra:\(\frac{16}{17^{19}+1}< \frac{16}{17^{18}+1}\)

             17A<17B

             A<B

Vậy A<B

\(\text{Ta có:}\frac{17^{18}+1}{17^{19}+1}\)

\(\Rightarrow17A=\frac{17^{19}+1+16}{17^{19}+1}\)

\(\Rightarrow17A=1+\frac{16}{17^{19}+1}\)

\(B=\frac{17^{17}+1}{17^{18}+1}\)

\(\Rightarrow17B=\frac{17^{18}+1+16}{17^{18}+1}\)

\(\Rightarrow17B=1+\frac{16}{17^{18}+1}\)

\(\text{Vì }\frac{16}{17^{19}+1}< \frac{16}{17^{18}+1}\)

\(\Rightarrow17A< 17B\)

\(\Rightarrow A< B\)

Ta có công thức :

\(\frac{a}{b}< \frac{a+c}{b+c}\left(\frac{a}{b}< 1;a,b,c\inℕ^∗\right)\)

Áp dụng vào ta có : 

\(A=\frac{17^{18}+1}{17^{19}+1}< \frac{17^{18}+1+16}{17^{19}+1+16}\)

\(=\frac{17^{18}+17}{17^{19}+17}\)

\(=\frac{17\left(17^{17}+1\right)}{17\left(17^{18}+1\right)}\)

\(\Leftrightarrow\frac{17^{17}+1}{17^{18}+1}\)'

\(\Rightarrow=B\)

Vậy \(A< B\)

Tham khảo :

\(17A=\dfrac{17^{19}+17}{17^{19}+1}=\dfrac{\left(17^{19}+1\right)+16}{17^{19}+1}=\dfrac{17^{19}+1}{17^{19}+1}+\dfrac{16}{17^{19}+1}=1+\dfrac{16}{17^{19}+1}\)

\(17B=\dfrac{17^{18}+17}{17^{18}+1}=\dfrac{\left(17^{18}+1\right)+16}{17^{18}+1}=\dfrac{17^{18}+1}{17^{18}+1}+\dfrac{16}{17^{18}+1}=1+\dfrac{16}{17^{18}+1}\)

Vì \(17^{19}>17^{18}=>17^{19}+1>17^{18}+1\)

\(=>\dfrac{16}{17^{19}+1}< \dfrac{16}{17^{18}+1}\)

\(=>17A< 17B=>A< B\)

A=(17^18+1)/(17^19+1)

17A=17(17^18+1)/17^19+1=17^19+17/17^19+1

17A=(17^19+1)+16/(17^19+1)=1+16/17^19+1    

B=(17^17+1)/(17^18+1)

17B=17(17^17+1)/17^18+1=17^18+17/17^18+1

17B=(17^18+1)+16/(17^18+1)=1+16/17^18+1

Từ (1) và (2)⇒1+16/17^19+1<1+16/17^18+1

=> 17A<17B

Hay A<B

Vậy A<B