Cho tam giác ABC có AC > AB, đường cao AD. Trong các khẳng định sau khẳng định nào sai?
A. ∠(ABC) > ∠(ACB)
B. BD < DC
C. Hình chiếu của A lên BC là D
D. ∠(BAD) > ∠(DAC)
Những câu hỏi liên quan
Cho hình chóp S.ABC có ABC là tam giác vuông tại A và SB vuông góc với mặt phẳng (ABC).Gọi BH là đường cao của tam giác SAB. Trong các khẳng định sau, khẳng định nào là khẳngđịnh sai?A. SA ⊥ BC. B. BH ⊥ SC. C. SA ⊥ AC. D. BH ⊥ AC.help me !!!
Đọc tiếp
Cho hình chóp S.ABC có ABC là tam giác vuông tại A và SB vuông góc với mặt phẳng (ABC).
Gọi BH là đường cao của tam giác SAB. Trong các khẳng định sau, khẳng định nào là khẳng
định sai?
A. SA ⊥ BC. B. BH ⊥ SC. C. SA ⊥ AC. D. BH ⊥ AC.
help me !!!
A là khẳng định sai.
Vì \(SB\perp\left(ABC\right)\) nên \(SB\perp BC\)
Nếu \(SA\perp BC\Rightarrow SA||SB\) hoặc SA trùng SB (đều vô lý)
Đúng 1
Bình luận (0)
Cho tam giác \(ABC\), biết \(DE//BC\) (Hình 2). Trong các khẳng định sau, khẳng định nào sai?
A. \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\).
B. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\).
C. \(\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
D. \(\frac{{BD}}{{AB}} = \frac{{DE}}{{BC}}\).
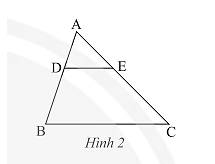
Vì \(DE//BC\) nên theo định lí Thales và hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\frac{{BD}}{{AD}} = \frac{{EC}}{{AE}};\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
Đúng 0
Bình luận (0)
Tam giác ABC có ∠A là góc tù, ∠B > ∠C. Trong các khẳng định sau, khẳng định nào đúng?
(A) AB > AC > BC
(B) AC > AB > BC
(C) BC > AB > AC
(D) BC > AC > AB
Do ∠A là góc tù nên ∠A lớn nhất. Vậy có ∠A> ∠B > ∠C. Từ đó suy ra BC > AC > AB. Chọn (D) BC > AC > AB.
Đúng 0
Bình luận (0)
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, AC vuông góc với mặt phẳng (ABC), AH là đường cao trong tam giác SAB. Trong các khẳng định sau, khẳng định nào là khẳng định sai? A.
A
H
⊥
A
C
B.
A
H
⊥
B
C
C.
S
A
⊥
B
C
D.
A
H
⊥
S
C
Đọc tiếp
Cho hình chóp SABC có đáy ABC là tam giác vuông tại B, AC vuông góc với mặt phẳng (ABC), AH là đường cao trong tam giác SAB. Trong các khẳng định sau, khẳng định nào là khẳng định sai?
A. A H ⊥ A C
B. A H ⊥ B C
C. S A ⊥ B C
D. A H ⊥ S C
Trong các khẳng định sau, khẳng định nào là đúng, khẳng định nào là sai ?
Các tam giác vuông ABC và DEF có ∠A=∠D=90o, AC=DE bằng nhau nếu có thêm :
a) BC = EF;
b) ∠C = ∠E;
c) ∠C = ∠F;
Xét hai tam giác vuông ABC và DFE có: ∠A = ∠D = 90º ; AC=DE
a) Thêm điều kiện BC=EF thì ΔABC=ΔDFE (cạnh huyền - cạnh góc vuông).
b) Thêm điều kiện ∠C = ∠E thì ΔABC=ΔDFE (g.c.g).
c) Thêm điều kiện ∠C = ∠F thì ta không thể kết luận ΔABC=ΔDFE
a) Đúng;
b) Đúng;
c) Sai.
Đúng 0
Bình luận (0)
Tam giác ABC có góc A tù, B ^ > C ^ . Trong các khẳng định sau, khẳng định nào đúng?
A. BC >AC >AB.
B. AC >AB >BC.
C. BC >AB > AC.
D. AB > AC > BC.
Cho tam giác cân ABC có đường cao
A
H
a
3
,
B
C
3
a
,BC chứa trong mặt phẳng (P). Gọi A’ là hình chiếu vuông góc của A lên mặt phẳng (P). Biết tam giác A’BC vuông tại A’. Gọi j là góc giữa (P) và (ABC). Chọn khẳng định đúng trong các khẳng định sau? A....
Đọc tiếp
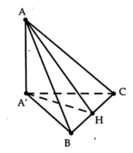
Cho tam giác cân ABC có đường cao A H = a 3 , B C = 3 a ,BC chứa trong mặt phẳng (P). Gọi A’ là hình chiếu vuông góc của A lên mặt phẳng (P). Biết tam giác A’BC vuông tại A’. Gọi j là góc giữa (P) và (ABC). Chọn khẳng định đúng trong các khẳng định sau?
A. φ = 30 o
B. φ = 45 o
C. cos φ = 2 3
D. φ = 60 o
Đáp án D
Ta có: B C ⊥ A A ' B C ⊥ A H
Do đó:
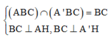
Mặt khác, tam giác A’BC vuông cân tại A’
nên A ' H = 1 2 B C = 3 a 2
Ta có:
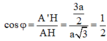
⇒ φ = 60 o
Đúng 0
Bình luận (0)
1) Cho tam giác ABC vuông tại A có đường cao AH . D và E lần lượt là điểm đối xứng của H qua AB , AC . Cho các khẳng định sau:1) D,A,E thẳng hàng2) BCED là hình thang3) BCED là hình thang cân 4) góc BAD góc CAF 5) góc DHE-90 độ khẳng định nào đúng?A. 1,3,4B. 1,3,5C. 1,2,5D. 1,2,3,4,5 2) Cho △ABC có AC 6 cm , BC 7 cm. Có thể tồn tại điểm M nằm trên đường phân giác của góc ngoài đỉnh C thỏa: A)AM 4cm, BM4cm B)AM 4cm, BM5cmC)AM+BM 13cmD)AM+BM13 cm
Đọc tiếp
1) Cho tam giác ABC vuông tại A có đường cao AH . D và E lần lượt là điểm đối xứng của H qua AB , AC . Cho các khẳng định sau:
1) D,A,E thẳng hàng
2) BCED là hình thang
3) BCED là hình thang cân
4) góc BAD= góc CAF
5) góc DHE-90 độ
khẳng định nào đúng?
A. 1,3,4
B. 1,3,5
C. 1,2,5
D. 1,2,3,4,5
2) Cho △ABC có AC = 6 cm , BC = 7 cm. Có thể tồn tại điểm M nằm trên đường phân giác của góc ngoài đỉnh C thỏa:
A)AM= 4cm, BM=4cm
B)AM = 4cm, BM=5cm
C)AM+BM> 13cm
D)AM+BM<13 cm
Cho tam giác ABC có BCa,ACb,ABc và bán kính đường tròn ngoại tiếp tam giác ABC bằng R. Tìm khẳng đính sai trong các khẳng định sau? A.
(
AB
→
,
BC
→
)
ABC
^
B.
S
Δ...
Đọc tiếp
Cho tam giác ABC có BC=a,AC=b,AB=c và bán kính đường tròn ngoại tiếp tam giác ABC bằng R. Tìm khẳng đính sai trong các khẳng định sau?
A. ( AB → , BC → ) = ABC ^
B. S Δ ABC = 1 2 bcsinA .
C. Nếu b 2 + c 2 – a 2 < 0 thì góc A là góc tù.
D. Nếu b+c=2a thì sinB+sin C=2sin A.
