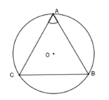
Cho tam giác ABC cân tại A có A ^ = 66 ° nội tiếp đường tròn (O) . Trong các cung nhỏ AB, BC, CA thì cung nào là cung lớn nhất?
A. AB
B. AC
C. BC
D. AB, AC
Cho tam giác ABC cân tại A có A ^ = 66 ° nội tiếp đường tròn (O) . Trong các cung nhỏ AB, BC, CA thì cung nào là cung lớn nhất?
A. AB
B. AC
C. BC
D. AB, AC
Chọn đáp án C.
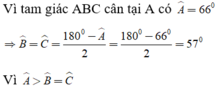
nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có:

Cho tam giác ABC cân tại A có góc A = 66° nội tiếp đường tròn (O) . Trong các cung nhỏ AB, BC, CA thì cung lớn nhất là
góc ABC=góc ACB=(180-66)/2=114/2=57 độ
=>góc BAC>góc ABC=góc ACB
=>Trong các cung nhỏ AB,BC,CA thì cung lớn nhất là cung BC
Cho tam giác ABC cân tại A nội tiếp trong đường tròn (O). Hãy so sánh các cung nhỏ AB, AC và BC biết A ^ = 50 0
Gợi ý: Đưa về so sánh góc ở tâm để kết luận
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa các cung bị chắn BC,CA,AB bởi các góc A,B,C. Có: AP⊥QR. Vẽ AP cắt CR tại I, ta được tam giác CPI là tam giác cân. Cho điểm A di chuyển trên cung lớn BC, hỏi I di chuyển trên đường nào?
Tui mứi học lớp 6 thui.......Xin lỗi...
Cho tam giác ABC cân đỉnh A nội tiếp trong đường tròn tâm O. Gọi M, N, P lần lượt là các điểm chỉnh giữa các cung nhỏ AB, BC, CA; BP cắt AN tại I; MN cắt AB tại E. Chứng minh rằng:
1. Tứ giác BCPM là hình thang cân; góc ABN có số đo bằng 900.
2. Tam giác BIN cân; EI // BC.
1: AB=AC
NB=NC
=>AN là trung trực của BC
mà O nằm trên trung trực của BC
nên A,N,O thẳng hàng
=>AN là đường kính của (O)
=>góc ABN=90 độ
2: góc BIN=1/2(sđ cung BN+sđ cung AP)
=1/2(sđ cungCN+sđ cung CP)
=1/2*sđ cung PN
=góc IBN
=>ΔIBN cân tại N
cho tam giác ABC nội tiếp đường tròn tâm O bán kính R có AB=\(R\sqrt{3}\) Và Cung CA = Cung CB . M là điểm bất kỳ trên cung nhỏ AB .
a) CM : MA+MB=MC
b) Tìm vị trí nhỏ nhất của M trên cung nhỏ BC để MA+MB là lớn nhất
Cho tam giác ABC không có góc tù (AB < AC), nội tiếp đường tròn (O; R). (B, C cố định, A di động trên cung lớn BC). Các tiếp tuyến tại B và C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC), cắt BC tại F, cắt AC tại I.
a) Chứng minh rằng MBIC là tứ giác nội tiếp.
b) Chứng minh rằng: FI.FM = FD.FE.
c) Đường thẳng OI cắt (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt (O) tại T (T khác Q). Chứng minh ba điểm P, T, M thẳng hàng.
d) Tìm vị trí điểm A trên cung lớn BC sao cho tam giác IBC có diện tích lớn nhất.

a) Do AB // DE nên \(\widebat{AE}=\widebat{BD}\Rightarrow\widebat{AE}+\widebat{DC}=\widebat{BD}+\widebat{DC}=\widebat{BC}\)
Ta có \(\widehat{MIC}\) là góc có đỉnh nằm trong đường tròn nên \(\widehat{MIC}=\frac{\widebat{AE}+\widebat{DC}}{2}=\frac{\widebat{BC}}{2}\)
Góc \(\widehat{MBC}\) là góc tạo bởi tiếp tuyến và dây cung nên \(\widehat{MBC}=\frac{\widebat{BC}}{2}\)
Suy ra \(\widehat{MIC}=\widehat{MBC}\)
Xét tứ giác BMCI có \(\widehat{MIC}=\widehat{MBC}\) nên BMCI là tứ giác nội tiếp.
b) Ta có \(\widehat{MIC}=\widehat{MBC}\Rightarrow\Delta FIC\sim\Delta FBM\left(g-g\right)\)
\(\Rightarrow\frac{FI}{FB}=\frac{FC}{FM}\Rightarrow FI.FM=FB.FC\)
Ta cũng có \(\widehat{DBF}=\widehat{CEF}\Rightarrow\Delta BFD\sim\Delta EFC\left(g-g\right)\)
\(\Rightarrow\frac{FB}{FE}=\frac{FD}{FC}\Rightarrow FE.FD=FB.FC\)
Vậy nên \(FI.FM=FE.FD\)
c) Do PQ là đường kính nên \(\widehat{PTQ}=90^o\)
Suy ra \(\Delta FIQ\sim\Delta FTM\left(c-g-c\right)\Rightarrow\widehat{FTM}=\widehat{FIQ}\)
Lại có BIMC nội tiếp, BOCM cũng nội tiếp nên 5 điểm B, O, I, C, M cùng thuộc đường trong đường kính OM.
Suy ra \(\widehat{FIQ}=90^o\)
Vậy thì P, T, M thẳng hàng.
d) Ta thấy \(S_{IBC}=\frac{1}{2}BC.d\left(I,BC\right)\)
Do BC không đổi nên SIBC lớn nhất khi d(I; BC) lớn nhất.
Điều này xảy ra khi I trùng O hay tam giác ABC vuông tại B.
Vậy diện tích tam giác IBC lớn nhất khi AC là đường kính đường tròn (O).
Cho tam giác ABC, không có góc tù (AB<AC) nội tiếp đường tròn (O;R). B,C cố định, A di động trên cung lớn BC . Các tiếp tuyến tại B,C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC ), cắt BC tại F, cắt AC tại K.
a) CMR:tứ giác MBOC nội tiếp
b) CMR: FK.FM=FD.FE
GIÚP MÌNH VỚI, MÌNH ĐANG CẦN GẤP !!
a)Xét tứ giác MBOC có
\(\widehat{OBM}\) và \(\widehat{OCM}\) là hai góc đối
\(\widehat{OBM}+\widehat{OCM}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: MBOC là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
1) Cho (O) và (I) lần lượt là đường tròn ngoại tiếp và đường tròn nội tiếp của tam giác ABC. Tia AI cắt (O) tại D, tia BI cắt (O) tại E, tia CI cắt (O) tại F (D khác A, E khác B, F khác C). Chứng minh rằng:
AD + BE + CF > AB + BC + CA
2) Cho tam giác cân ABC nội tiếp trong đường tròn (O;R) (AB = AC và BAC = 300). Gọi D là điểm thuộc cung nhỏ AB sao cho cung BD = 300, E là điểm thuộc cung nhỏ AC sao cho DE = AB và EA < EC, DE cắt AB và AC lần lượt tại M và N. Tính: AB và AM theo R.