Chọn đáp án C.
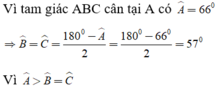
nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có:

Chọn đáp án C.

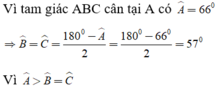
nên theo mối liên hệ giữa cạnh và góc trong tam giác ta có:

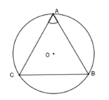
Cho tam giác ABC cân tại A có A ^ = 66 ° nội tiếp đường tròn (O) . Trong các cung nhỏ AB, BC, CA thì cung nào là cung lớn nhất?
A. AB
B. AC
C. BC
D. AB, AC
Cho tam giác ABC cân tại A có góc A = 66° nội tiếp đường tròn (O) . Trong các cung nhỏ AB, BC, CA thì cung lớn nhất là
Cho tam giác ABC cân tại A nội tiếp trong đường tròn (O). Hãy so sánh các cung nhỏ AB, AC và BC biết A ^ = 50 0
Cho tam giác ABC, không có góc tù (AB<AC) nội tiếp đường tròn (O;R). B,C cố định, A di động trên cung lớn BC . Các tiếp tuyến tại B,C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC ), cắt BC tại F, cắt AC tại K.
a) CMR:tứ giác MBOC nội tiếp
b) CMR: FK.FM=FD.FE
GIÚP MÌNH VỚI, MÌNH ĐANG CẦN GẤP !!
Cho tam giác ABC không có góc tù (AB < AC), nội tiếp đường tròn (O; R). (B, C cố định, A di động trên cung lớn BC). Các tiếp tuyến tại B và C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC), cắt BC tại F, cắt AC tại I.
a) Chứng minh rằng MBIC là tứ giác nội tiếp.
b) Chứng minh rằng: FI.FM = FD.FE.
c) Đường thẳng OI cắt (O) tại P và Q (P thuộc cung nhỏ AB). Đường thẳng QF cắt (O) tại T (T khác Q). Chứng minh ba điểm P, T, M thẳng hàng.
d) Tìm vị trí điểm A trên cung lớn BC sao cho tam giác IBC có diện tích lớn nhất.
1) Cho (O) và (I) lần lượt là đường tròn ngoại tiếp và đường tròn nội tiếp của tam giác ABC. Tia AI cắt (O) tại D, tia BI cắt (O) tại E, tia CI cắt (O) tại F (D khác A, E khác B, F khác C). Chứng minh rằng:
AD + BE + CF > AB + BC + CA
2) Cho tam giác cân ABC nội tiếp trong đường tròn (O;R) (AB = AC và BAC = 300). Gọi D là điểm thuộc cung nhỏ AB sao cho cung BD = 300, E là điểm thuộc cung nhỏ AC sao cho DE = AB và EA < EC, DE cắt AB và AC lần lượt tại M và N. Tính: AB và AM theo R.
Cho tam giác ABC cân tại B nội tiếp trong đường tròn tâm O. Biết góc C=30 độ,hay so sánh các cung nhỏ AB,AC và BC
Cho tam giác ABC không có góc tù (AB<AC), nội tiếp đường tròn (O;R).(B, C cố định, A di động trên cung lớn BC). Các tiếp tuyến tại B và C cắt nhau tại M. Từ M kẻ đường thẳng song song với AB, đường thẳng này cắt (O) tại D và E (D thuộc cung nhỏ BC ), cắt BC tại F, cắt AC tại I
a) C/m : góc MBC = BAC . Từ đó suy ra MBIC là tứ giác nội tiếp.
b) C/m : FI.FM = FD.FE
c) Đường thẳng OI cắt (o) tại P và Q (P thuộc cung nhỏ AB ). Đường thẳng QF cắt (O) tại T (T khác Q ). C/m : 3 điểm P, T, M thẳng hàng
d) Tìm vị trí điểm A trên cung lớn BC sao cho tam giác IBC có diện tích lớn nhất
Cho tam giác ABC cân tại A, góc A < 90 độ, một cung tròn BC nằm trong tam giác ABC và tiếp xúc với AB, AC tại B và C. Trên cung BC lấy một điểm M rồi hạ đường vuông góc MI, MH, MK xuống các cạnh BC, CA, AB. Gọi P là giao điểm của MB và IK , Q là giao điểm của MC, IH.
a) CM tứ giác BIMK, CIMH nội tiếp
b) CM tia đối của tia MI là phân giác của góc HMK
c) CM tứ giác MPIQ nội tiếp