Cho đường thẳng d x = 1 - 2 t y = 2 + t z = 3 - t và mặt phẳng P : 2 x + y + z = 0 . Tìm tọa độ giao điểm A của d và (P)
A. A 15 4 ; - 10 4 ; 5 4
B. A - 2 ; 1 ; 1
C. A - 10 4 ; 15 4 ; 5 4
D. A 1 ; 2 ; - 4
Những câu hỏi liên quan
Trong không gian Oxyz, cho hai đường thẳng
d
:
x
1
+
t
y
2
-
t
z...
Đọc tiếp
Trong không gian Oxyz, cho hai đường thẳng d : x = 1 + t y = 2 - t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d, d ' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x - 1 - 2 = y - 2 1 = z 3
B. x - 4 - 2 = y - 1 = z - 2 3
C. x 2 = y - 3 - 1 = z + 1 - 3
D. x - 2 - 2 = y - 1 1 = z - 1 3
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
:
x
1
+
t
y
2
-
t...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d : x = 1 + t y = 2 - t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d, d' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x - 1 - 2 = y - 2 1 = z 3
B. x - 4 - 2 = y - 1 = z - 2 3
C. x 2 = y - 3 - 1 = z + 1 - 3
D. x - 2 - 2 = y - 1 1 = z - 1 3
Đáp án D
HD: Để AB nhỏ nhất <=> AB là đoạn vuông góc chung của d, d'
Gọi A ∈ d => A(1+a;2-a;a) và B ∈ d => B(2b,1+b;2+b) ⇒ A B → = ( 2 b - a - 1 ; a + b - 1 ; b - a + 2 )
Vì A B ⊥ d A B ⊥ d ' ⇒ A B → . u d → A B → . u d ' → ⇔ 2 b - a - 1 - a - b + 1 + b - a + 2 = 0 2 ( 2 b - a - 1 ) + a + b - 1 + b - a + 2 = 0
⇔ - 3 a + 2 b + 2 = 0 - 2 a + 6 b - 1 = 0 ⇔ a = 1 b = 1 2
Vậy A(2;1;1), B 1 ; 3 2 ; 5 2 ⇒ A B → = - 1 ; 1 2 ; 3 2 = - 1 2 2 ; - 1 ; - 3
⇒ ( A B ) : x - 2 - 2 = y - 1 1 = z - 1 3
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
x
1
+
t
y
2
−
t
z
t
,...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng x = 1 + t y = 2 − t z = t , d ' : x = 2 t ' y = 1 + t ' z = 2 + t ' . Đường thẳng ∆ cắt d , d ' lần lượt tại các điểm A, B thỏa mãn độ dài đoạn thẳng AB nhỏ nhất. Phương trình đường thẳng ∆ là
A. x − 1 − 2 = y − 2 1 = z 3 .
B. x − 4 − 2 = y − 1 = z − 2 3 .
C. x 2 = y − 3 − 1 = z + 1 − 3 .
D. x − 2 − 2 = y − 1 1 = z − 1 3 .
1. Cho d: x - y + 3 0 , overrightarrow{v} (2; -1)a1) Toverrightarrow{v}(d) d . Viết phương trình đường thẳng da2) Toverrightarrow{v}(d) d. Viết phương trình đường thẳng d2. * left(x-1right)^2+left(y+3right)^22** x^2+y^2-4x+2y+10overrightarrow{v} (3;2)Tìm ảnh của (C) qua Toverrightarrow{v}
Đọc tiếp
1. Cho d: x - y + 3 = 0 , \(\overrightarrow{v}\)= (2; -1)
a1) T\(\overrightarrow{v}\)(d) = d' . Viết phương trình đường thẳng d'
a2) T\(\overrightarrow{v}\)(d') = d. Viết phương trình đường thẳng d'
2. * \(\left(x-1\right)^2+\left(y+3\right)^2=2\)
** \(x^2+y^2-4x+2y+1=0\)
\(\overrightarrow{v}\) = (3;2)
Tìm ảnh của (C) qua T\(\overrightarrow{v}\)
Không hiểu câu hỏi số 2 của em
Ở đây có 2 pt đường tròn khác nhau, vậy (C) là cái nào trong 2 cái trên? Hoặc đề yêu cầu tìm ảnh của cả 2 đường tròn?
Đúng 0
Bình luận (1)
1.
a/ Gọi \(M\left(x;y\right)\) là 1 điểm bất kì thuộc d \(\Rightarrow x-y+3=0\) (1)
Gọi \(M'\left(x';y'\right)\) là ảnh của M qua phép tịnh tiến vecto \(\overrightarrow{v}\Rightarrow M'\in d'\)
Theo công thức tọa độ phép tịnh tiến:
\(\left\{{}\begin{matrix}x'=x+2\\y'=y-1\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=x'-2\\y=y'+1\end{matrix}\right.\)
Thế vào (1) \(\Rightarrow\left(x'-2\right)-\left(y'+1\right)+3=0\)
\(\Leftrightarrow x'-y'=0\)
Vậy pt d' có dạng: \(x-y=0\)
b/ Tương tự như trên, vẫn gọi \(M'\left(x';y'\right)\) là điểm thuộc d' và \(M\left(x;y\right)\) là ảnh của M' qua phép tịnh tiến
\(\Rightarrow M\in d\Rightarrow x-y+3=0\) (2)
Theo công thức tọa độ phép tịnh tiến:
\(\left\{{}\begin{matrix}x=x'+2\\y=y'-1\end{matrix}\right.\) thế vào (2):
\(x'+2-\left(y'-1\right)+3=0\Leftrightarrow x'-y'+6=0\)
Vậy pt d' có dạng: \(x-y+6=0\)
Đúng 0
Bình luận (0)
2.
a. Đường tròn (C) có tâm \(I\left(1;-3\right)\) và bán kính \(R=\sqrt{2}\)
Gọi \(\left(C'\right)\) có tâm \(I'\left(x';y'\right)\) bán kính \(R'\) là ảnh của (C) qua phép tịnh tiến
\(\Rightarrow R'=R=\sqrt{2}\) và I' là ảnh của I qua phép tịnh tiến \(\overrightarrow{v}\)
\(\Rightarrow\left\{{}\begin{matrix}x'=x_I+3=4\\y'=y_I+2=-1\end{matrix}\right.\)
Phương trình (C'): \(\left(x-4\right)^2+\left(y+1\right)^2=2\)
b. Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=2\)
...trình bày tương tự như trên:
\(\left\{{}\begin{matrix}x'=x_I+3=5\\y'=y_I+2=1\end{matrix}\right.\)
Phương trình (C'): \(\left(x-5\right)^2+\left(y-1\right)^2=4\)
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x1-2t ; y1+t; zt+2 (t ∈ R). Tìm một véc-tơ chỉ phương của đường thẳng d. A. (-2;1;2) B. (-2;1;1) C. (1;1;1) D. (2;-1;-2).
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng d: x=1-2t ; y=1+t; z=t+2 (t ∈ R). Tìm một véc-tơ chỉ phương của đường thẳng d.
A. (-2;1;2)
B. (-2;1;1)
C. (1;1;1)
D. (2;-1;-2).
Đáp án B
Đường thẳng d có vec tơ chỉ phương là 
Đúng 0
Bình luận (0)
Cho các đường thẳng d1: x+y+3=0 , d2: x-y-4=0 , d3: x-2y=0. Tìm tọa độ điểm M nằm trên đường thẳng d3 sao cho khoảng cách từ M đến đường thẳng d1 bằng hai lần khoảng cách từ M đến đường thẳng d2
Do \(M\in d_3\) \(\Rightarrow M\left(2a;a\right)\)
\(\frac{\left|2a+a+3\right|}{\sqrt{1^2+1^2}}=2\frac{\left|2a-a-4\right|}{\sqrt{1^2+\left(-1\right)^2}}\Leftrightarrow\left|3a+3\right|=2\left|a-4\right|\)
\(\Leftrightarrow\left(3a+3\right)^2=4\left(a-4\right)^2\Leftrightarrow9a^2+18a+9=4a^2-32a+64\)
\(\Leftrightarrow5a^2+50a-55=0\Rightarrow\left[{}\begin{matrix}a=1\\a=-11\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(2;1\right)\\M\left(-22;-11\right)\end{matrix}\right.\)
Đúng 0
Bình luận (1)
Vẽ hình 22 vào vở rồi tìm điểm Z trên đường thẳng d1 và điểm T trên đường thẳng d2 sao cho X, Z, T thẳng hàng và Y, Z, T thẳng hàng
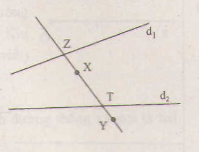Ba điểm X,Z,T thẳng hàng vậy X nằm trên đường thẳng ZT.
- Ba điểm Y,Z,T thẳng hàng vì vậy Y nằm trên đường thẳng ZT.
Suy ra X,Y nằm trên đường thẳng ZT, dó đó 4 điểm Z,Y,Z,T thẳng hàng.
Các vẽ: vẽ đường thẳng XY cắt đường thẳng d1 tài Z , cắt đường thẳng d2 tại T
Đúng 0
Bình luận (0)
Giải:
- Ba điểm X,Z,T thẳng hàng vậy X nằm trên đường thẳng ZT.
- Ba điểm Y,Z,T thẳng hàng vì vậy Y nằm trên đường thẳng ZT.
Suy ra X,Y nằm trên đường thẳng ZT, dó đó 4 điểm Z,Y,Z,T thẳng hàng.
Các vẽ: vẽ đường thẳng XY cắt đường thẳng d1 tài Z , cắt đường thẳng d2 tại T
Đúng 0
Bình luận (0)
Cho đường thẳng y=(m-2).x + m + 1 (d)
a)Vẽ (d) khi m=1
b)Tìm m để đường thẳng (d) // đường thẳng y= 2x -1
c)Với giá trị m tìm được ở câu b,hãy tìm tọa độ giao điểm của đường thẳng (d) với đường thẳng y =3x+2
-PLS GIÚP MÌNH VỚI Ạ HUHU-
Xem thêm câu trả lời
Cho đường thẳng d: x 1 + t, y 2 - t, z 1 + at và mặt phẳng (P): 2x + y + z + b 0. Tìm a và b để đường thẳng d nằm trong mặt phẳng (P) A. a 1; b -5 B. a -1, b 5 C. a -1, b -5 D. Không tồn tại a, b thỏa mãn
Đọc tiếp
Cho đường thẳng d: x = 1 + t, y = 2 - t, z = 1 + at và mặt phẳng (P): 2x + y + z + b = 0. Tìm a và b để đường thẳng d nằm trong mặt phẳng (P)
A. a = 1; b = -5
B. a = -1, b = 5
C. a = -1, b = -5
D. Không tồn tại a, b thỏa mãn
Cho ba đường thẳng y = 2x (d1) ; y = x + 1 (d2) ; y = (k - 2)x + 2k + 1 (d3)
Tìm k để ba đường thẳng trên đồng quy