Giả sử hai nghiệm của phương trình 2 x 2 + 2 x = 8 là x 1 , x 2 x 1 < x 2 . Khi đó x 1 - 2 x 2 có giá trị là
A. -4
B. 7
C. 6
D. -5
2. Cho phương trình x^2 + mx + m - 1 (m là tham số). (1)
a) Giải phương trình khi m = 5
b) Chứng minh phương trình (1) luôn có nghiệm với mọi giá trị của m. Giả sử x1,x2 là hai nghiệm của phương trình (1), tìm giá trị nhỏ nhất của biểu thức: Q = x1^2 + x2^2 = 4x1 - 4x2.
a: Khi m=5 thì (1) sẽ là: x^2+5x+4=0
=>x=-1; x=-4
b: Sửa đề: Q=x1^2+x2^2-4x1-4x2
Q=(x1+x2)^2-2x1x2-4(x1+x2)
=m^2-2(m-1)-4(-m)
=m^2-2m+2+4m
=m^2+2m+2=(m+1)^2+1>=1
Dấu = xảy ra khi m=-1
Giả sử phương trình Ax2+Bx+C=0 có hai nghiệm x1, x2 thì x + x=-B/A, x*x=C/A. Cho a khác 0 và giả sử phương trình x2 - ax - 1/2a2. Chứng minh rằng x14+x24 >=2+√2
đoạn sau là x2-ax-1/(2a2)=0 nha, viết thiếu.
@nguyenthanhtuan cái này là chứng minh mà bạn.
Giả sử x là nghiệm của phương trình 4 1 x - 2 = ln e 2 . Tính lnx
A. 0
B. ln3
C. -ln3
D. 1
Để ý rằng
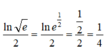
nên phương trình đã cho tương đương với
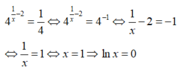
Chọn đáp án A.
Cho hệ phương trình 5 x + 2 y = - 3 3 x + y = - 2
Giả sử (x;y) là nghiệm của hệ phương trình, khi đó - x . y 3 bằng
A. -1.
B. 1
C. 2
D. -2
giả sử a,b là nghiệm của phương trình \(x^2+px+1=0\)
giả sử c,d là nghiệm của phương trình \(x^2+qx+1=0\)
chứng minh hệ thức: (a-c)(a+d)(b+d)=\(q^2-p^2\)
Cho phương trình x 2 - 2 ( m - 1 ) x + m 2 - 3 m = 0 Giả sử phương trình có hai nghiệm x 1 ; x 2 .Tìm hệ thức giữa x 1 ; x 2 độc lập đối với m.
![]()
![]()
![]()
![]()
Đáp án: A
Theo hệ thức Vi-ét ta có: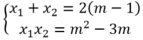
Ta xét các phương án:
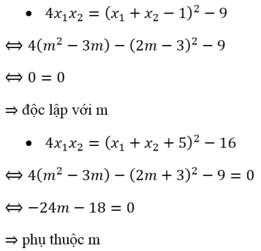
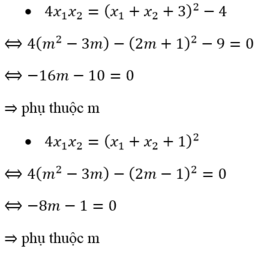
giả sử phương trình bậc 2 : x^2 + ax + b + 1 = 0 có hai nghiệm nguyên dương. chứng minh rằng : a^2 + b^2 là 1 hợp số
gọi x1,x2 là hai nghiệm \(\Rightarrow x_1+x_2=-a\) và \(x_1x_2=b+1\)
Ta có : \(a^2+b^2=\left[-\left(x_1+x_2\right)\right]^2+\left(x_1x_2-1\right)^2\)
\(\Rightarrow a^2+b^2=\left(x_1^2+x_2^2+2x_1x_2\right)+\left(x_1^2x_2^2-2x_1x_2+1\right)\)
\(\Rightarrow a^2+b^2=x_1^2+x_2^2+x_1^2x_2^2+1=\left(x_1^2+1\right)\left(x_2^2+1\right)\)là hợp số
giả sử (x0,y0) là nghiệm của hệ phương trình \(\left\{{}\begin{matrix}x^2+y^2=25\\x+y-xy=-5\end{matrix}\right.\)
Cho phương trình bậc 2 x^2- 2( m-1) x+m^2=0
1.Tìm m để:
A.Pt có hai nghiệm phân biệt
B. PT có một nghiệm là -2
2. Giả sử X1, x2 là 2 nghiệm của PT. cmt (x1-x2) ^2+4(x1+x2) +4=0
giả sử a,b là 2 nghiệm của phương trình: x^2 + mx +1 =0 và b,c là 2 nghiệm của pt: x^2 + nx + 2 =0.
Chứng minh: (b-a)(b-c)=mn-6
Theo hệ thức Vi - ét
=> a+ b = - m và a.b = 1
b + c= - n và b.c = 2
Ta có : m .n = (-m). (-n) = (a+b). (b +c)
= [(b - a) + 2a)]. [(b- c) + 2c)] = (b - a).( b - c) + 2c( b - a) + 2a.( b - c) + 4ac
= (b - a).( b - c) + 2bc - 2ac + 2ab - 2ac + 4ac
= (b - a).( b - c) + 2.2 + 2.1 = (b - a).( b - c) + 6
=> (b - a).( b - c) =m.n - 6 (ĐPCM)