Cho tam giác ABC đều cạnh a. Mệnh đề nào sau đây đúng?
A.![]()
B.![]()
C. ![]()
D. ![]()
Cho tam giác ABC đều cạnh a. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Chọn C.
Độ dài các cạnh của tam giác là a thì độ dài các vectơ
![]()
Cho tam giác đều ABC cạnh a=2. Hỏi mệnh đề nào sau đây sai
A. B C → . C A → = - 2
B. B C → - A C → B A → = 2
C. A B → + B C → A C → = 4
D. A B → . A C → B C → = 2 B C →
Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sau đây sai?
![]()
![]()
![]()
![]()
Chọn C.
Ta có : ![]()
Ta đi xét các phương án:
Phương án A: ![]() nên
nên ![]()
Loại A.
Phương án B: ![]()
Loại B.
Phương án C: ![]()
![]()
Chọn C.
Cho một tam giác ABC đều tâm O. Gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Mệnh đề nào sau đây đúng?
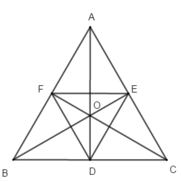
A. Q ( 0 ; 120 o ) ( ∆ O D C ) = ∆ O F A
B. Q ( 0 ; 120 o ) ( ∆ A O F ) = ∆ B O D
C. Q ( 0 ; 120 o ) ( ∆ A O B ) = ∆ A O C
D. Q ( 0 ; 60 o ) ( ∆ O F E ) = ∆ O D E
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA = a 3 và vuông góc với mặt đáy (ABC). Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng?
A. φ = 30 o
B. sin φ = 5 5
C. φ = 60 o
D. sin φ = 2 5 5
Chọn D.
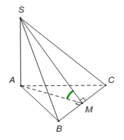
Gọi M là trung điểm của BC, suy ra AM ⊥ BC.
Ta có
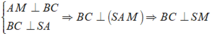
Do đó
![]()
Tam giác ABC đều cạnh a, suy ra trung tuyến AM = a 3 2
Tam giác vuông SAM, có
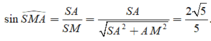
Cho tam giác ABC là tam giác đều. Mệnh đề nào sau đây đúng?
A. ![]()
B. ![]()
C. ![]()
D. ![]()
Chọn D.
+ Phương án A: Do ![]()
Loại A.
+ Phương án B: ![]() và
và ![]() nên
nên ![]()
Loại B.
+ Phương án C: Do ![]() và
và ![]() không cùng phương.
không cùng phương.
Loại C.
+ Phương án D: AB = BC = CA 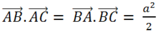
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Cạnh bên SA vuông góc với mặt đáy (ABC) và S A = a 3 . Gọi φ là góc giữa hai mặt phẳng (SBC) và (ABC). Mệnh đề nào sau đây đúng?
A. φ = 30 °
B. φ = 60 °
C. sin φ = 5 5
D. sin φ = 2 5 5
Gọi M là trung điểm BC, suy ra A M ⊥ B C
Tam giác ABC đều cạnh a suy ra trung tuyến ![]()
Tam giác vuông SAM có ![]()
Chọn D.
Cho tam giác \(ABC\). Lấy điểm \(M\) trên cạnh \(AC\) kéo dài (Hình 1). Mệnh đề nào sau đây là mệnh đề sai?
A. \(M \in \left( {ABC} \right)\).
B. \(C \in \left( {ABM} \right)\).
C. \(A \in \left( {MBC} \right)\).
D. \(B \in \left( {ACM} \right)\).
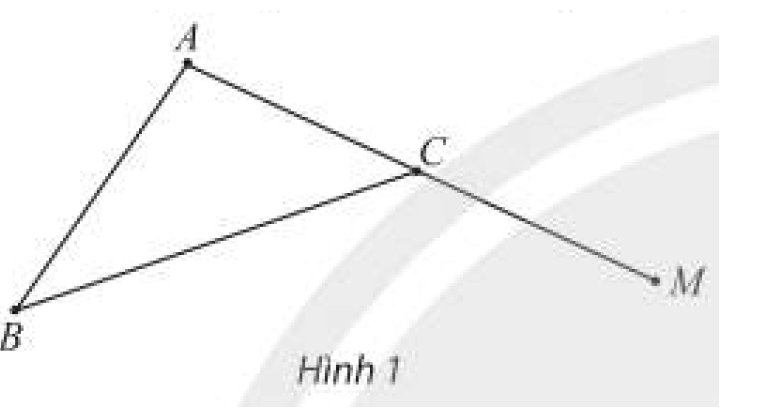
\(\left. \begin{array}{l}M \in AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow M \in \left( {ABC} \right)\). Vậy mệnh đề A đúng.
\(\left. \begin{array}{l}C \in AM\\AM \subset \left( {ABM} \right)\end{array} \right\} \Rightarrow C \in \left( {ABM} \right)\). Vậy mệnh đề B đúng.
\(\left. \begin{array}{l}A \in CM\\CM \subset \left( {MBC} \right)\end{array} \right\} \Rightarrow A \in \left( {MBC} \right)\). Vậy mệnh đề C đúng.
Vậy mệnh đề D sai.
Chọn D.
3. Cho a, b, c là độ dài ba cạnh của một tam giác.
Mệnh đề nào sau đây không đúng?
A. a 2 < a b + a c
B. a b + b c > b 2
C. b 2 + c 2 < a 2 + 2 b c
D. b 2 + c 2 > a 2 + 2 b c
Do a, b, c là độ dài ba cạnh của một tam giác nên theo bất đẳng thức tam giác ta có:
* a < b + c ⇔ a 2 < a b + c ⇔ a 2 < a b + a c
* a + c > b ⇔ b a + c > b 2 ⇔ a b + b c > b 2
* b - c < a ⇔ b - c 2 < a 2 ⇔ b 2 - 2 b c + c 2 < a 2 ⇔ b 2 + c 2 < a 2 + 2 b c
Do đó, mệnh đề D không đúng.