Chọn D.
+ Phương án A: Do ![]()
Loại A.
+ Phương án B: ![]() và
và ![]() nên
nên ![]()
Loại B.
+ Phương án C: Do ![]() và
và ![]() không cùng phương.
không cùng phương.
Loại C.
+ Phương án D: AB = BC = CA 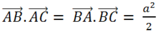
Chọn D.
+ Phương án A: Do ![]()
Loại A.
+ Phương án B: ![]() và
và ![]() nên
nên ![]()
Loại B.
+ Phương án C: Do ![]() và
và ![]() không cùng phương.
không cùng phương.
Loại C.
+ Phương án D: AB = BC = CA 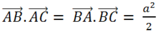
Cho tam giác ABC đều cạnh a. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Biết A ; B ; C là các góc của tam giác ABC , mệnh đề nào sau đây đúng:
A. sin( A + C) = - sinB
B. cos( A + B) = - cos C
C. tan (A + C) = tanB
D. cot( A+ C) = cot B
Cho tam giác ABC. Xét các mệnh đề dạng P ⇒ Q sau
a)Nếu ABC là một tam giác đều thì ABC là một tam giác cân.
b)Nếu ABC là một tam giác đều thì ABC là một tam giác cân và có một góc bằng 60o
Hãy phát biểu các mệnh đề Q ⇒ P tương ứng và xét tính đúng sai của chúng.
Cho tam giác đều ABC và điểm I thỏa mãn I A → = 2 I B → . Mệnh đề nào sau đây đúng?
A. C I → = C A → − 2 C B → 3 .
B. C I → = C A → + 2 C B → 3 .
C. C I → = − C A → + 2 C B → .
D. C I → = C A → + 2 C B → − 3 .
Cho tam giác ABC. Mệnh đề nào sau đây là đúng?
A. Với mọi điểm E trên đường thẳng BC, vectơ A E → không cùng phương với vectơ B C → .
B. Vectơ A E → có thể cùng phương với vectơ B C → .
C. Tập hợp các điểm M sao cho A M → cùng phương với B C → là một đường thẳng qua A.
D. Tập hợp các điểm N sao cho A N → cùng hướng với B C → là đường thẳng qua A, song song với BC.
Cho tam giác đều ABC cạnh a = 2. Hỏi mệnh đề nào sau đây sai?
![]()
![]()
![]()
![]()
Trong các mệnh đề sau
a. Nếu tam giác ABC thỏa mãn AB2 + AC2 = BC2 thì tam giác ABC vuông tại B.
b. Nếu một phương trình bậc hai có biệt thức không âm thì nó có nghiệm.
c. Tam giác ABC là tam giác đều khi và chỉ khi nó thỏa mãn đồng thời hai điều kiện AB = AC và góc A = 600.
d. Hình thang cân có một trục đối xứng.
Các mệnh đề đúng là:
A. a, c.
B. a, b, c.
C. b, c.
D. b, c, d.
Cho tam giác ABC, với M là trung điểm BC. Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
3. Cho a, b, c là độ dài ba cạnh của một tam giác.
Mệnh đề nào sau đây không đúng?
A. a 2 < a b + a c
B. a b + b c > b 2
C. b 2 + c 2 < a 2 + 2 b c
D. b 2 + c 2 > a 2 + 2 b c