Xét tính tăng, giảm và bị chặn của dãy số u n , biết: u n = 2 n - 13 3 n - 2
A. Dãy số tăng, bị chặn
B. Dãy số giảm, bị chặn
C. Dãy số không tăng không giảm, không bị chặn
D. Cả A, B, C đều sai
Xét tính tăng, giảm và bị chặn của các dãy số u n , biết: u n = n + 1 - n
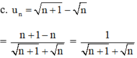
+ Xét tính tăng giảm.
Với mọi n ∈ N ta có:
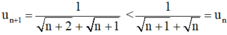
⇒ un + 1 < un với mọi n ∈ N.
⇒ (un) là dãy số giảm.
+ Xét tính bị chặn.
un > 0 với mọi n.
⇒ (un) bị chặn dưới.
un ≤ u1 = √2 - 1 với mọi n
⇒ (un) bị chặn trên.
⇒ (un) bị chặn.
Xét tính tăng, giảm và bị chặn của các dãy số u n , biết: u n = n + 1 n
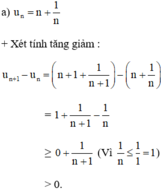
⇒ un + 1 > un với mọi n ∈ N
⇒ (un) là dãy tăng.
+ Xét tính bị chặn:
(un) là dãy tăng
⇒ u1 = 2 < u2 < u3 < …< un ∀n ∈ N*
⇒ un ≥ 2 ∀n ∈ N*
⇒ (un) bị chặn dưới.
(un) không bị chặn trên.
⇒ un không bị chặn.
Xét tính tăng, giảm và bị chặn của dãy số ( u n ) , biết: u n = 1 1 + n + n 2
A. Dãy số tăng, bị chặn trên
B. Dãy số tăng, bị chặn dưới
C. Dãy số giảm, bị chặn
D. Cả A, B, C đều sai
Ta có: u n > 0 ∀ n ≥ 1
u n + 1 u n = n 2 + n + 1 ( n + 1 ) 2 + ( n + 1 ) + 1 = n 2 + n + 1 n 2 + 3 n + 3 < 1 ∀ n ∈ ℕ *
⇒ u n + 1 < u n ∀ ≥ 1 ⇒ dãy ( u n ) là dãy số giảm.
Mặt khác: 0 < u n < 1 ⇒ dãy ( u n ) là dãy bị chặn.
Chọn đáp án C
Xét tính tăng hay giảm và bị chặn của dãy số : u n = 2 n − 1 n + 3 ; n ∈ N *
A. Dãy số giảm, bị chặn trên
B. Dãy số tăng, bị chặn dưới
C. Dãy số tăng, bị chặn.
D. Dãy số giảm, bị chặn dưới.
Xét hiệu: u n + 1 − u n = 2 n + 1 n + 4 − 2 n − 1 n + 3
= 2 n 2 + 7 n + 3 − 2 n 2 − 7 n + 4 n + 4 n + 3 = 7 n + 4 n + 3 > 0 ; ∀ n ∈ N *
Vậy: ( u n ) là dãy số tăng.
Ta có u n = 2 n − 1 n + 3 = 2 ( n + 3 ) − 7 n + 3 = 2 − 7 n + 3
Suy ra: ∀ n ∈ ℕ * , u n < 2 nên ( u n ) bị chặn trên.
Vì ( u n ) là dãy số tăng ∀ n ∈ ℕ * , u 1 = 1 4 ≤ u n nên ( u n ) bị chặn dưới. Vậy ( u n ) bị chặn.
Chọn đáp án C.
Xét tính tăng giảm và bị chặn của dãy số sau: (un) u 1 = 2 u n + 1 = u n + 1 2 , ∀ n ≥ 2
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn B.
Trước hết bằng quy nạp ta chứng minh: (un) 1 < un ≤ 2, ∀ n
Điều này đúng với n = 2, giả sử 1 < un < 2 ta có: ![]() nên ta có đpcm.
nên ta có đpcm.
Mà ![]() .
.
Vậy dãy (un) là dãy giảm và bị chặn.
Xét tính tăng, giảm và bị chặn của dãy số u n , biết: u n = 2 n n !
A. Dãy số tăng, bị chặn trên
B. Dãy số tăng, bị chặn dưới
C. Dãy số giảm, bị chặn trên
D. Cả A, B, C đều sai
Cho dãy số (Un), với un = 1/1×2+ 1/2×3 + 1/3×4 +...+ 1/n(n+1). Xét tính tăng, giảm và bị chặn của dãy số.
\(u_n=\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{n\left(n+1\right)}\)
\(=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{n}-\dfrac{1}{n+1}\)
\(=1-\dfrac{1}{n+1}< 1\)
=>Hàm số bị chặn trên tại \(u_n=1\)
\(n+1>=1\)
=>\(\dfrac{1}{n+1}< =1\)
=>\(-\dfrac{1}{n+1}>=-1\)
=>\(1-\dfrac{1}{n+1}>=-1+1=0\)
=>Hàm số bị chặn dưới tại 0
\(u_n=1-\dfrac{1}{n+1}=\dfrac{n+1-1}{n+1}=\dfrac{n}{n+1}\)
\(\dfrac{u_n}{u_{n+1}}=\dfrac{n}{n+1}:\dfrac{n+1}{n+2}=\dfrac{n^2+2n}{n^2+2n+1}< 1\)
=>(un) là dãy số tăng
Xét tính tăng, giảm, bị chặn của dãy số (un) với un = 1/n+1
\(u_n=\dfrac{1}{n+1}\Rightarrow u_{n+1}=\dfrac{1}{n+2}\)
\(\Rightarrow u_n-u_{n+1}=\dfrac{1}{n+1}-\dfrac{1}{n+2}=\dfrac{1}{\left(n+1\right)\left(n+2\right)}>0\)
\(\Rightarrow u_{n+1}< u_n\Rightarrow\) dãy giảm
Do \(\dfrac{1}{n+1}>0\Rightarrow\) dãy bị chặn dưới bởi 0
\(u_n-1=\dfrac{1}{n+1}-1=-\dfrac{n}{n+1}< 0\Rightarrow u_n< 1\)
\(\Rightarrow\) Dãy bị chặn trên bởi 1
\(\Rightarrow\) Dãy bị chặn
Xét tính tăng giảm và bị chặn của các dãy số sau: u 1 = 2 ; u 2 = 3 u n + 1 = u n + u n - 1 , ∀ n ≥ 2
A. Tăng, bị chặn
B. Giảm, bị chặn
C. Tăng, chặn dưới
D. Giảm, chặn trên
Chọn A.
Trước hết ta chứng minh 1 < un < 4
Điều này hiển nhiên đúng với n = 1.
Giả sử 1 < un < 4, ta có: ![]()
Ta chứng minh (un) là dãy tăng
Ta có u1 < u2, giả sử un-1 < un, ∀ n ≤ k.
Khi đó: 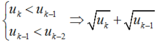
![]()
Vậy dãy (un) là dãy tăng và bị chặn.
Xét tính tăng, giảm và bị chặn của dãy số biết u n = 1 + 1 2 2 + 1 3 2 + ... + 1 n 2
A. Dãy số tăng, bị chặn dưới.
B. Dãy số tăng, bị chặn.
C. Dãy số giảm, bị chặn trên.
D. Tất cả đều sai.
Đáp án B
Ta có
u n + 1 = 1 + 1 2 2 + 1 3 2 + ... + 1 n 2 + 1 n + 1 2 = u n + 1 n + 1 2 > u n ,
vậy dãy số đã cho là dãy số tăng.
Hơn nữa vì dãy số là tổng các số dương nên bị chặn dưới bởi 0, ta chỉ cần kiểm tra dãy số có bị chặn trên hay không là đủ để chọn phương án đúng.
Ta có
1 2 2 < 1 1.2 = 1 − 1 2 1 3 2 < 1 2.3 = 1 2 − 1 3 .......................... 1 n 2 < 1 n − 1 . n = 1 n − 1 − 1 n
Vì vậy u n < 2 − 1 n < 2 , do đó dãy số bị chặn trên.