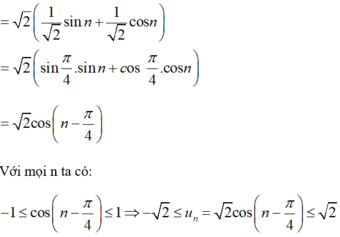B ị   c h ặ n   d ư ớ i   v ì   u n   ≥   2 ,   ∀ n   ∈   N ∗

B ị   c h ặ n   d ư ớ i   v ì   u n   ≥   3 ,   ∀ n   ∈   N ∗

B ị   c h ặ n   v ì   0   <   u n   ≤   1 / 2 ,   ∀ n   ∈   N ∗

un = sin n + cos n.

un = 2n2 – 1

+ Với n ∈ N* ta có: n ≥ 1 và n2 ≥ 1

⇒ un = 2n2 – 1 ≥ 2.12 – 1 = 1.

⇒ un ≥ 1

⇒ dãy (un) bị chặn dưới ∀n ∈ N*.

+ (un) không bị chặn trên vì không có số M nào thỏa mãn:

un = 2n2 – 1 ≤ M ∀n ∈N*.

Vậy dãy số (un) bị chặn dưới và không bị chặn trên nên không bị chặn.

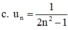
+ Ta có : 2n2 – 1 > 0 ∀ n ∈ N*

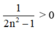⇒  ∀ n ∈ N*.

⇒ (un) bị chặn dưới.

+ 2n2 – 1 ≥ 2.1 – 1 = 1

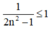⇒  ∀ n ∈ N*

⇒ (un) bị chặn trên.

Vậy (un) bị chặn.

Ta có : 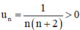 ∀ n ≥ 1.

⇒ (un) bị chặn dưới

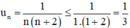 ∀ n ≥ 1.

⇒ (un) bị chặn trên.

Vậy (un) là dãy bị chặn.

a) Ta có: \(n \ge 1\; \Rightarrow n - 1 \ge 0\; \Rightarrow {u_n} \ge 0,\;\forall \;n \in {N^*}\;\)

Do đó, \(\left( {{u_n}} \right)\) bị chặn dưới bởi 0.

\(\left( {{u_n}} \right)\) không bị chặn trên vì không tồn tại số M nào để \(n - 1 < M,\;\forall \;n \in {N^*}\).

b) Ta có:

\(\begin{array}{l}\forall n \in {N^*},{u_n} = \frac{{n + 1}}{{n + 2}} > 0.\\{u_n} = \frac{{n + 1}}{{n + 2}} = \frac{{n + 2 - 1}}{{n + 2}} = 1 - \frac{1}{{n + 2}} < 1,\forall n \in {N^*}\\ \Rightarrow 0 < {u_n} < 1\end{array}\)

Vậy \(\left( {{u_n}} \right)\) bị chặn.

c) Ta có: 

\( - 1 < \sin n < 1\)

\( \Rightarrow  - 1 < {u_n} < 1,\forall n \in {N^*}\)

Vậy \(\left( {{u_n}} \right)\) bị chặn.

d) Ta có: 

Nếu n chẵn, \({u_n} =  - {n^2} < 0\), \(\forall n \in {N^*}\).

Nếu n lẻ, \({u_n} = {n^2} > 0\), \(\forall n \in {N^*}\).

Vậy \(\left( {{u_n}} \right)\) không bị chặn.

Chọn A

• Ta có: \({u_{n + 1}} = \frac{{\left( {n + 1} \right) + 1}}{{\left( {n + 1} \right) + 2}} = \frac{{n + 1 + 1}}{{n + 1 + 2}} = \frac{{n + 2}}{{n + 3}}\)

Xét hiệu:

\(\begin{array}{l}{u_{n + 1}} - {u_n} = \frac{{n + 2}}{{n + 3}} - \frac{{n + 1}}{{n + 2}} = \frac{{{{\left( {n + 2} \right)}^2} - \left( {n + 1} \right)\left( {n + 3} \right)}}{{\left( {n + 3} \right)\left( {n + 2} \right)}} = \frac{{\left( {{n^2} + 4n + 4} \right) - \left( {{n^2} + n + 3n + 3} \right)}}{{\left( {n + 2} \right)\left( {n + 1} \right)}}\\ = \frac{{{n^2} + 4n + 4 - {n^2} - n - 3n - 3}}{{\left( {n + 2} \right)\left( {n + 1} \right)}} = \frac{1}{{\left( {n + 2} \right)\left( {n + 1} \right)}} > 0,\forall n \in {\mathbb{N}^*}\end{array}\)

Vậy \({u_{n + 1}} - {u_n} > 0 \Leftrightarrow {u_{n + 1}} > {u_n}\). Vậy dãy số \(\left( {{u_n}} \right)\) là dãy số tăng.

• Ta có: \({u_n} = \frac{{n + 1}}{{n + 2}} = \frac{{\left( {n + 2} \right) - 1}}{{n + 2}} = 1 - \frac{1}{{n + 2}}\)

\(\forall n \in {\mathbb{N}^*}\) ta có:

\(n + 2 > 0 \Leftrightarrow \frac{1}{{n + 2}} > 0 \Leftrightarrow 1 - \frac{1}{{n + 2}} < 1 \Leftrightarrow {u_n} < 1\). Vậy \(\left( {{u_n}} \right)\) bị chặn trên.

\(n \ge 1 \Leftrightarrow n + 2 \ge 1 + 2 \Leftrightarrow n + 2 \ge 3 \Leftrightarrow \frac{1}{{n + 2}} \le \frac{1}{3} \Leftrightarrow 1 - \frac{1}{{n + 2}} \ge 1 - \frac{1}{3} \Leftrightarrow {u_n} \ge \frac{2}{3}\)

Vậy \(\left( {{u_n}} \right)\) bị chặn dưới.

Ta thấy dãy số \(\left( {{u_n}} \right)\) bị chặn trên và bị chặn dưới nên dãy số \(\left( {{u_n}} \right)\) bị chặn.

Chọn A.