Giải phương trình: 2x3 + 6x2 = x2 + 3x

Những câu hỏi liên quan
Giải phương trình
a) 2x3+6x2=x2+3x
b) (2+x)2-(2x-5)2=0
`2x^3 +6x^2 =x^2 +3x`
`<=> 2x^3 +6x^2 -x^2 -3x=0`
`<=> 2x^3 +5x^2 -3x=0`
`<=> x(2x^2 +5x-3)=0`
`<=> x(2x^2 +6x-x-3)=0`
`<=> x[2x(x+3)-(x+3)]=0`
`<=> x(2x-1)(x+3)=0`
\(< =>\left[{}\begin{matrix}x=0\\2x-1=0\\x+3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=-3\end{matrix}\right.\)
b)
`(2+x)^2 -(2x-5)^2=0`
`<=> (2+x-2x+5)(2+x+2x-5)=0`
`<=> (-x+7)(3x-3)=0`
\(< =>\left[{}\begin{matrix}-x+7=0\\3x-3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
`a) 2x^3 + 6x^2 = x^2 + 3x`
`=> 2x^3 + 6x^2 - x^2 - 3x = 0`
`=> 2x^3 + 5x^2 - 3x = 0`
`=> x(2x^2 + 5x - 3) = 0`
`=> x (2x^2 + 6x - x - 3) = 0`
`=> x [(2x^2 + 6x) - (x+3)] = 0`
`=> x [2x(x+3) - (x+3)] = 0`
`=> x (2x - 1)(x+3) = 0`
`=> x = 0` hoặc `2x - 1 = 0` hoặc `x + 3 = 0`
`=> x = 0` hoặc `x = 1/2` hoặc `x = -3`
`b) (2+x)^2 - (2x-5)^2 = 0`
`=> (2+x+2x-5)(2+x-2x+5) = 0`
`=> (3x - 3)(7-x) = 0`
`=> 3x - 3 = 0` hoặc `7 - x = 0`
`=> x = 1` hoặc `x = 7`
Đúng 0
Bình luận (0)
giúp mình bài này với
giải phương trình :
a) 2x3=6x2=x2+3x;2x3+6x2=x2+3x;
b) (3x-1)(x2+2)= (3x-1)(7x-10)(3x-1)(x2+2)=((3x-1)(7x-10)
giải phương trình:
a, x4-x2-2=0
b, x4+2x3+x2=0
c,x3-1= 0
d, 6x2-7x+2=0
a, \(x^4-x^2-2=0\Leftrightarrow x^4-2x^2+x^2-2=0\)
\(\Leftrightarrow x^2\left(x^2-2\right)+\left(x^2-2\right)=0\Leftrightarrow\left(x^2+1>0\right)\left(x^2-2\right)=0\Leftrightarrow x=\pm\sqrt{2}\)
b, \(\Leftrightarrow x^2\left(x^2+2x+1\right)=0\Leftrightarrow x^2\left(x+1\right)^2=0\Leftrightarrow x=0;x=-1\)
c, \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1>0\right)=0\Leftrightarrow x=1\)
d, \(\Leftrightarrow6x^2-3x-4x+2=0\Leftrightarrow\left(3x-2\right)\left(2x-1\right)=0\Leftrightarrow x=\dfrac{2}{3};x=\dfrac{1}{2}\)
Đúng 2
Bình luận (0)
a)
/ \(x^4+x^2-2=0\)
\(\Leftrightarrow\left(x^2\right)^2-x^2+2x^2-2=0\\ \Leftrightarrow x^2\left(x^2-1\right)+2\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x^2-1\right)=0\\ \Leftrightarrow\left(x^2+2\right)\left(x-1\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2+2=0\\x+1=0\\x-1-0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Câu 6:Thực hiện phép nhân -2x(x2 + 3x - 4) ta được:A.-2x3 - 6x2 – 8x B. 2x3 -6x2 – 8x C. -2x3 - 6x2 + 8x D. -2x3 + 3x2 -4Câu 7 : Phân tích đa thức x2 + 2xy + y2 – 9z2 thành nhân tử ta được:A. (x+y+3z)(x+y–3z) B. (x-y+3z)(x+y–3z) C.(x - y +3z)(x - y – 3z)D. (x + y +3z)(x -y – 3z)Câu 8: Phân tích đa thức 27x3 – thành nhân tử ta được:A.(3x+)(9x2-x+) B.(3x–)(9x2+x+) C.(27x–)(9x2+x+) D.(27x+)(9x2+x+) Câu 9: Phân tích đa thức x2 + 7x + 12 thành nhân tử ta được:A. (x - 3)( x...
Đọc tiếp
Câu 6:Thực hiện phép nhân -2x(x2 + 3x - 4) ta được:
A.-2x3 - 6x2 – 8x B. 2x3 -6x2 – 8x C. -2x3 - 6x2 + 8x D. -2x3 + 3x2 -4
Câu 7 : Phân tích đa thức x2 + 2xy + y2 – 9z2 thành nhân tử ta được:
A. (x+y+3z)(x+y–3z)
B. (x-y+3z)(x+y–3z)
C.(x - y +3z)(x - y – 3z)
D. (x + y +3z)(x -y – 3z)
Câu 8: Phân tích đa thức 27x3 – ![]() thành nhân tử ta được:
thành nhân tử ta được:
A.(3x+![]() )(9x2-x+
)(9x2-x+![]() )
)
B.(3x–![]() )(9x2+x+
)(9x2+x+![]() )
)
C.(27x–![]() )(9x2+x+
)(9x2+x+![]() )
)
D.(27x+![]() )(9x2+x+
)(9x2+x+![]() )
)
Câu 9: Phân tích đa thức x2 + 7x + 12 thành nhân tử ta được:
A. (x - 3)( x + 4 ) B. (x + 3)( x + 4 ) C.(x + 5)( x + 2 ) D. (x -5)( x + 2 )
Câu 10: Giá trị của biểu thức (x2 + 4x + 4) tại x = - 2 là:
A. 4 B. -2 C. 0 D. -8
Câu 6:Thực hiện phép nhân -2x(x2 + 3x - 4) ta được:
A.-2x3 - 6x2 – 8x B. 2x3 -6x2 – 8x C. -2x3 - 6x2 + 8x D. -2x3 + 3x2 -4
Câu 7 : Phân tích đa thức x2 + 2xy + y2 – 9z2 thành nhân tử ta được:
A. (x+y+3z)(x+y–3z)
B. (x-y+3z)(x+y–3z)
C.(x - y +3z)(x - y – 3z)
D. (x + y +3z)(x -y – 3z)
Câu 9: Phân tích đa thức x2 + 7x + 12 thành nhân tử ta được:
A. (x - 3)( x + 4 ) B. (x + 3)( x + 4 ) C.(x + 5)( x + 2 ) D. (x -5)( x + 2 )
Câu 10: Giá trị của biểu thức (x2 + 4x + 4) tại x = - 2 là:
A. 4 B. -2 C. 0 D. -8
Mấy câu còn lại bị lỗi r nhé
Đúng 1
Bình luận (0)
Giải các phương trình:
a
)
2
x
3
−
x
2
+
3
x
+
6
0
b
)
x
(
x...
Đọc tiếp
Giải các phương trình:
a ) 2 x 3 − x 2 + 3 x + 6 = 0 b ) x ( x + 1 ) ( x + 4 ) ( x + 5 ) = 12

b) x.(x+1). ( x+ 4). (x+ 5) = 12
⇔ [ x. (x + 5)]. [(x+1). (x+ 4)] = 12
⇔ x 2 + 5 x ⋅ x 2 + 4 x + x + 4 − 12 = 0 ⇔ x 2 + 5 x ⋅ x 2 + 5 x + 4 − 12 = 0 ( * )
Đặt t = x 2 + 5 x + 2
= > x 2 + 5 x = t – 2 v à x 2 + 5 x + 4 = t + 2
Khi đó phương trình (*) trở thành:
( t – 2). (t+ 2) - 12 = 0
⇔ t 2 − 4 − 12 = 0 ⇔ t 2 − 16 = 0 ⇔ t 2 = 16 ⇔ t = ± 4
+ Với t = 4 ta có: x 2 + 5 x + 2 = 4
⇔ x 2 + 5 x – 2 = 0 ( * * )
Có a= 1, b = 5, c = - 2 và ∆ = 5 2 – 4 . 1 . ( - 2 ) = 33 > 0
Nên (**) có 2 nghiệm phân biệt là:
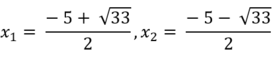
* Với t = - 4 ta có: x 2 + 5 x + 2 = - 4
⇔ x 2 + 5 x + 6 = 0 ( * * * )
Có a= 1, b = 5, c= 6 và ∆ = 5 2 – 4 . 1 . 6 = 1 > 0
Phương trình (***) có 2 nghiệm là:
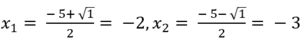
Vậy tập nghiệm của phương trình đã cho là:
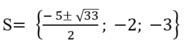
Đúng 0
Bình luận (0)
Giải các phương trình:
a
)
2
x
3
−
x
2
+
3
x
+
6
0
b
)
x
(
x...
Đọc tiếp
Giải các phương trình:
a ) 2 x 3 − x 2 + 3 x + 6 = 0 b ) x ( x + 1 ) ( x + 4 ) ( x + 5 ) = 12

b) x.(x+1). ( x+ 4). (x+ 5) = 12
⇔ [ x. (x + 5)]. [(x+1). (x+ 4)] = 12
⇔ x 2 + 5 x ⋅ x 2 + 4 x + x + 4 − 12 = 0 ⇔ x 2 + 5 x ⋅ x 2 + 5 x + 4 − 12 = 0 ( * )
Đặt t = x 2 + 5 x + 2
= > x 2 + 5 x = t – 2 v à x 2 + 5 x + 4 = t + 2
Khi đó phương trình (*) trở thành:
( t – 2). (t+ 2) - 12 = 0
⇔ t 2 - 4 - 12 = 0 ⇔ t 2 - 16 = 0 ⇔ t 2 = 16 ⇔ t = ± 4
+ Với t = 4 ta có: x 2 + 5 x + 2 = 4
⇔ x2 +5x – 2 = 0 (**)
Có a= 1, b = 5, c = - 2 và ∆ = 5 2 – 4 . 1 . ( - 2 ) = 33 > 0
Nên (**) có 2 nghiệm phân biệt là:
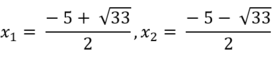
* Với t = - 4 ta có: x 2 + 5 x + 2 = - 4
⇔ x 2 + 5 x + 6 = 0 ( * * * )
Có a= 1, b = 5, c= 6 và ∆ = 5 2 – 4 . 1 . 6 = 1 > 0
Phương trình (***) có 2 nghiệm là:
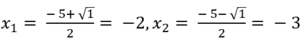
Vậy tập nghiệm của phương trình đã cho là:
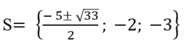
Đúng 0
Bình luận (0)
Giải phương trình
x
2
-
3
x
+
6
x
2
-
9
1
x
-
3
Bằng cách điền vào các chỗ trống (…) và trả lời các câu hỏi.- Điều kiện: x ≠ …- Khử mẫu và bi...
Đọc tiếp
Giải phương trình
x 2 - 3 x + 6 x 2 - 9 = 1 x - 3
Bằng cách điền vào các chỗ trống (…) và trả lời các câu hỏi.
- Điều kiện: x ≠ …
- Khử mẫu và biến đổi, ta được: x2 – 3x + 6 = … ⇔ x2 – 4x + 3 = 0.
- Nghiệm của phương trình x2 – 4x + 3 = 0 là: x1 = …; x2 = …
Hỏi x1 có thỏa mãn điều kiện nói trên không ? Tương tự, đối với x2 ?
Vậy nghiệm của phương trình đã cho là:....
- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x2 – 3x + 6 = x + 3 ⇔ x2 – 4x + 3 = 0.
- Nghiệm của phương trình x2 – 4x + 3 = 0 là: x1 = 1; x2 = 3
x1 có thỏa mãn điều kiện nói trên
x2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1
Đúng 0
Bình luận (0)
Giải phương trình
x
2
−
3
x
+
6
x
2
−
9
1
x
−
3
Bằng cách điền vào các chỗ trống (…) và trả lời các câu hỏi.- Điều kiện: x ≠ …- Khử mẫu và biến đổi, ta được:
x
2...
Đọc tiếp
Giải phương trình
x 2 − 3 x + 6 x 2 − 9 = 1 x − 3
Bằng cách điền vào các chỗ trống (…) và trả lời các câu hỏi.
- Điều kiện: x ≠ …
- Khử mẫu và biến đổi, ta được: x 2 – 3 x + 6 = … ⇔ x 2 – 4 x + 3 = 0 .
- Nghiệm của phương trình x 2 – 4 x + 3 = 0 l à : x 1 = … ; x 2 = …
Hỏi x 1 có thỏa mãn điều kiện nói trên không ? Tương tự, đối với x 2 ?
Vậy nghiệm của phương trình đã cho là:....
- Điều kiện: x ≠ ±3
- Khử mẫu và biến đổi, ta được: x 2 – 3 x + 6 = x + 3 ⇔ x 2 – 4 x + 3 = 0 .
- Nghiệm của phương trình x 2 – 4 x + 3 = 0 l à : x 1 = 1 ; x 2 = 3
x 1 có thỏa mãn điều kiện nói trên
x 2 không thỏa mãn điều kiện nói trên
Vậy nghiệm của phương trình đã cho là: x = 1
Đúng 0
Bình luận (0)
Hãy giải các phương trình sau đây :
1, x2 - 4x + 4 = 0
2, 2x - y = 5
3, x + 5y = - 3
4, x2 - 2x - 8 = 0
5, 6x2 - 5x - 6 = 0
6,( x2 - 2x )2 - 6 (x2 - 2x ) + 5 = 0
7, x2 - 20x + 96 = 0
8, 2x - y = 3
9, 3x + 2y = 8
10, 2x2 + 5x - 3 = 0
11, 3x - 6 = 0
1) Ta có: \(x^2-4x+4=0\)
\(\Leftrightarrow\left(x-2\right)^2=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
Vậy: S={2}
Đúng 1
Bình luận (0)



















