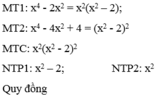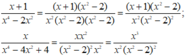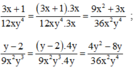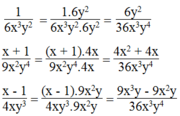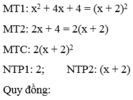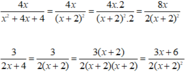Quy đồng mẫu thức các phân thức sau: 11 102 x 4 y ; 3 34 x y 3

Những câu hỏi liên quan
Quy đồng mẫu thức các phân thức sau x x - y ; x+y
MT1: x – y
MT2: 1
MTC: x – y
NTP1: 1; NTP2: x – y.
Quy đồng:
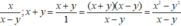
Đúng 0
Bình luận (0)
Quy đồng mẫu thức các phân thức sau x + 1 x 4 - 2 x 2 ; x x 4 - 4 x 2 + 4
Quy đồng mẫu thức các phân thức sau 1/3x+xy, 2y+2x và 1/x^2+2xy+y^2
\(\dfrac{1}{3x+xy}=\dfrac{1}{x\left(y+3\right)}=\dfrac{\left(x+y\right)^2}{x\left(y+3\right)\left(x+y\right)^2}\)
\(2x+2y=2\left(x+y\right)=\dfrac{2\left(x+y\right)\cdot x\left(y+3\right)\left(x+y\right)^2}{x\left(y+3\right)\left(x+y\right)^2}\)
\(\dfrac{1}{x^2+2xy+y^2}=\dfrac{3x+xy}{x\left(y+3\right)\left(x+y\right)^2}\)
Đúng 2
Bình luận (0)
quy đồng mẫu thức các phân thức sau 1/3x+3y, 1/2y+2x và 1/x^2+2xy+y^2
\(\dfrac{1}{3x+3y}=\dfrac{1}{3\left(x+y\right)}=\dfrac{2\cdot\left(x+y\right)}{6\left(x+y\right)^2}\)
\(\dfrac{1}{2x+2y}=\dfrac{1}{2\left(x+y\right)}=\dfrac{3\left(x+y\right)}{6\left(x+y\right)^2}\)
\(\dfrac{1}{x^2+2xy+y^2}=\dfrac{1}{\left(x+y\right)^2}=\dfrac{6}{6\left(x+y\right)^2}\)
Đúng 0
Bình luận (1)
Quy đồng mẫu thức các phân thức sau:
3
x
+
1
12
x
y
4
;
y
-
2
9
x
2
y
3
Đọc tiếp
Quy đồng mẫu thức các phân thức sau: 3 x + 1 12 x y 4 ; y - 2 9 x 2 y 3
Quy đồng mẫu thức các phân thức sau 1 6 x 3 y 2 , x + 1 9 x 2 y 4
M T C : 18 x 3 y 4 N T P 1 : 3 y 2 ; N T P 2 : 2 x
Quy đồng:
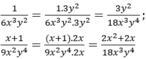
Đúng 0
Bình luận (0)
Quy đồng mẫu thức các phân thức sau
a) 25/14x^2y và 14/21xy^5
b)11/102x^4y và 3/34xy^3
c)3x+1/12xy^4 và y-2/9x^2y^3
Quy đồng mẫu thức các phân thức sau:
1
6
x
3
y
2
;
x
+
1
9
x
2
y
4
;
x
-
1
4
x...
Đọc tiếp
Quy đồng mẫu thức các phân thức sau: 1 6 x 3 y 2 ; x + 1 9 x 2 y 4 ; x - 1 4 x y 3
Quy đồng mẫu thức các phân thức sau 4 x x 2 + 4 x + 4 ; 3 2 x + 4
Quy đồng mẫu thức các phân thức sau: a) 1/x^2y và 3/xy b) x/(x^2+2xy+y^2) và 2x/(x^2+xy)
a: 1/x^2y=1/x^2y
3/xy=3x/x^2y
b: \(\dfrac{x}{x^2+2xy+y^2}=\dfrac{x}{\left(x+y\right)^2}\)
\(\dfrac{2x}{x^2+xy}=\dfrac{2}{x+y}=\dfrac{2x+2y}{\left(x+y\right)^2}\)
Đúng 2
Bình luận (1)