Cho tam giác ABC, vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số đồng dạng k = 2/3.

Những câu hỏi liên quan
Cho tam giác ABN đồng dạng với tam giác A'B'C' theo tỉ số đồng dạng 2/3. Tam giác A'B'C' đồng dạng với tam giác A"B"C" theo tỉ số đồng dạng 3/4. Tính tỉ số đồng dạng của tam giác A"B"C" và tam giác ABC
Xem chi tiết
Sửa đề: ΔABC\(\sim\)ΔA'B'C' theo tỉ số đồng dạng \(k_1=\dfrac{2}{3}\)
Vì ΔABC\(\sim\)ΔA'B'C' theo tỉ số đồng dạng \(k_1=\dfrac{2}{3}\)
mà ΔA'B'C' \(\sim\)ΔA''B''C'' theo tỉ số đồng dạng \(k_2=\dfrac{3}{4}\)
nên ΔABC\(\sim\)ΔA''B''C'' theo tỉ số đồng dạng \(k_1\cdot k_2=\dfrac{2}{3}\cdot\dfrac{3}{4}=\dfrac{2}{4}=\dfrac{1}{2}\)
hay ΔA"B"C"\(\sim\)ΔABC theo tỉ số đồng dạng k=2
Đúng 3
Bình luận (0)
Cho tam giác ABC, vẽ tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ lệ đồng dạng \(k=\dfrac{2}{3}\)
Giải:
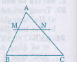
Trên cạnh AB lấy điểm M sao cho AM= AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=
Dựng ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)
Đúng 0
Bình luận (0)
Trên cạnh AB lấy điểm M sao cho AM= 232323AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=232323
Dựng ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)
Đúng 0
Bình luận (0)
Trên cạnh AB lấy điểm M sao cho AM= \(\dfrac{2}{3}\)AB.
Từ m kẻ đường song song với AB cắt AC tại N.
Ta có ∆AMN ∽ ∆ABC theo tỉ số đồng dạng K=\(\dfrac{2}{3}\)
Dựng ∆A'B'C' = ∆AMN(theo trường hợp cạnh cạnh cạnh)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) có đồng dạng với tam giác \(ABC\) không? Tỉ số đồng dạng là bao nhiêu?
b) Cho tam giác \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng \(k\) thì \(\Delta ABC\backsim\Delta A'B'C'\) theo tỉ số nào?
a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).
Đúng 1
Bình luận (0)
Vẽ tam giác A'B'C' đồng dạng tam giác ABC theo tỉ số k=1/2 b) trên tam giác ABC lấy điểm M, qua M kẻ MN//BC tam giác ABC đồng dạng Tam giác AMN không?tại sao?
b: Xét ΔAMN và ΔABC có
\(\widehat{AMN}=\widehat{ABC}\)(đồng vị, MN//BC)
góc A chung
Do đó: ΔAMN\(\sim\)ΔABC
Đúng 2
Bình luận (1)
Đúng hay Sai
1. tam giác MNP đồng dạng EGF thì MN/NP = EG/FG
2. cho tam giác A'B'C' đồng dạng với tam giác ABC với tỉ số đồng dạng là k=2 khi đó tỉ số chu vi tam giác ABC so với chu vi tam giác A'B'C' là 2
Cho tam giác ABC vẽ tam giác A’B’C’ đồng dạng với tam giác ABC theo tỉ số đồng dạng là K = 2/3.
Cho tam giác A'B'C' đồng dạng với tam giác ABC theo tỉ số k = 4/3.Tính chu vi của tam giác ABC, biết chu vi của tam giác A'B'C' bằng 27 cm
cho tam giác abc đồng dạng với tam giác a'b'c' theo tỉ số k=2 thì tỉ số đường cao của 2 tam giác đó bằng
Cho tam giác đồng dạng với tam giác ABC theo tỉ số k = 4/3. Tính chu vi của tam giác ABC, biết chu vi của tam giác A'B'C' bằng 27cm.
Ta có Δ A'B'C' ∈ Δ ABC theo tỉ số k
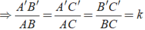
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
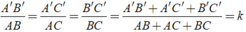
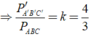
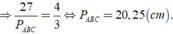
Đúng 0
Bình luận (0)