Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng: ∠A = ∠B + ∠C.
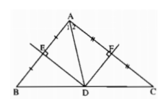
Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng:
D là trung điểm của cạnh BC.
Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
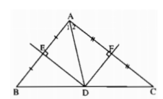
Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng :
a) D là trung điểm của cạnh BC
b) \(\widehat{A}=\widehat{B}+\widehat{C}\)
a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b)
Ta có ∆DEB = ∆DEA(c.g.c) nên ˆB=ˆA1B^=A1^. Tương tự ˆC=ˆA2C^=A2^.
Suy ra ˆA=ˆA1+ˆA2=ˆB+ˆC
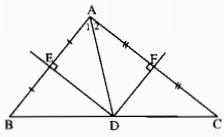
Cho tam giác ABC,hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC.Chứng minh rằng:
a. D là trung điểm của cạnh BC
b. Số đo góc A = tổng số đo góc B và góc C

a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b) Ta có: Tam giác DEA = tam giác DEA (c.g.c) nên góc B = góc A1
<=> góc C = góc A2
=> Góc A = góc A1 + góc A2 = góc B + góc C.
l
a) Gọi M, N lần lượt là giao điểm của các đường trung trực tương ứng với các cạnh AB và AC.
Ta có: MD vuông góc với AB và ND vuông góc với AC ⇒ AMDN là hình chữ nhật (tứ giác có 2 góc đối bằng 90 độ)
⇒ AN = MD và AM = ND (1)
mà AN = NC; AM = MB (M, N lần lượt là trung điểm của Ab và AC) (2)
Từ (1) và (2) ⇒ NC = MD và MB = ND
Xét tam giác BMD và tam giác DNC, ta có:
+ MB = ND (cmt)
+ góc BMD = góc DNC ( = 90 độ)
+ MD = NC
Suy ra: tam giác BMD = tam giác DNC (c.g.c)
⇒ BD = DC ⇒ D là trung điểm của BC. (đpcm)
b) Tứ giác AMDN là hình chữ nhật (câu a) ⇒ Góc MAN = 90 độ. (*)
Trong tam giác vuông DNC có: góc NDC + góc NCD = 90 độ (vuông tại N) (3)
mà góc MBD = góc NCD (góc tương ứng của 2 tam giác bằng nhau) (4)
Từ (3), (4) ⇒ góc MBD + góc NCD = 90 độ (**)
Từ (*) và (**) suy ra: góc MBD + góc NCD = góc MAN
hay: Số đo góc A bằng tổng số đo góc B và góc C. (đpcm)
trong tam giác ABC hai đường trung trực của hai cạnh AB và AC cắt nhau tại D nằm trên cạnh BC . chứng minh rằng :
a) D là trung điểm của cạnh BC
b) góc A= góc B +góc C
Cho tam giác ABC, hai đường trung trực của 2 cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh AB.Chứng minh rằng:
a) D là trung điểm của cạnh BC
b) Số đo góc A bằng tổng số đo góc B và góc C
Trong tam giác ABC, hai đường trung trực của hai cạnh AB và AC cắt nhau tại điểm D nằm trên cạnh BC. Chứng minh rằng:
a) Dlà trung điểm của canh BC
b) Góc A bằng góc B cộng góc C.
a) Vì D là điểm chung của 2 dường trung trực
=>D là điểm chung của 3 đường trung trực (tính đồng quy trong tam giác)
=>D thuộc trung trực ứng với cạnh BC mà D thuộc BC
=> D là trung điểm của cạnh BC (đpcm)
b) Nối AD
Vì D là điểm chung của 3 trung trực (câu a) mà D thuộc BC
=> tam giác ABC vuông tại A (tam giác có tâm đường tròn ngoại tiếp thuộc 1 cạnh của tam giác ấy là tam giác vuông)
=>góc B +góc C = góc A = 90 độ (t/c tam giác vuông) (đpcm)
Cho tam giác ABC vuông tại A, có AB > AC. Đường trung trực của cạnh huyền BC cắt AB tại D. M là một điểm tùy ý trên đoạn BD. Chứng minh rằng:
a, Điểm D nằm giữa hai điểm A và B
b, DB < CM
ôi dào , bài nhu thế này ta ko bt làm , phải làm sao đây ....?
Cho tam giác ABC có AC> AB. Trên cạnh AC lấy điểm D sao cho CD = AB. Đường trung trực của AD và đường trung trực của BC cắt nhau ở E. Chứng minh rằng điểm E nằm trên đường tròn ngoại tiếp tam giác ABC
Xét hai tam giác ABE và DCE có AB=DC (giả thiết), BE=CE (vì E nằm trên trung trực BC) và EA=ED (vì E nằm trên trung trực CD). Suy ra hai tam giác bằng nhau theo trường hợp c.c.c. Từ đó suy ra góc ABE= góc DCE = góc ACE. Vậy B,C nhìn AE dưới hai góc bằng nhau, do đó ABCE nội tiếp. Suy ra E nằm trên đường tròn ngoại tiếp tam giác ABC.
Cho tam giác ABC có AB < AC. Trên cạnh AC lấy điểm D sao cho CD = AB. Hai đường trung trực của BD và AC cắt nhau tại E. Chứng minh:
a) ∆ B E = ∆ C D E ;
b) Điểm E cách đều hai cạnh AB và AC.