Các câu hỏi tương tự
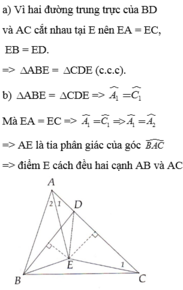
cho tam giác ABC có AB<AC. Trên cạnh AC lấy điểm D sao cho CD=AB. Hai đường trung trực của BD và AC cắt nhau tại E. Chứng minh rằng tam giác AEB= tam giác CED
cho tam giác ABC có AB<AC. Trên cạnh AC lấy điểm D sao cho CD=AB. Hai đường trung trực của BD và AC cắt nhau tại E. Chứng mình rằng:
a) tam giác AEB= tam giác CED
b) AE là tia phân giác trong tại đỉnh A của tam giác ABC
Cha tam giác ABC (AB<AC). Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho BD=CE. Các đường trung trực của BC và DE cắt nhau tại O. Chứng minh tam giác BOD = tam giác COE
cho tam giác ABC cân tại A ,hai đường trung trực của AB và AC cắt nhau tại M .Trên cạnh AB lấy điểm D và trên cạnh AC lấy điểm E sao cho AD =CE.
a,chứng minh MD=ME
b,Khi D di chuyển trên cạnh AB và AC sao cho AD =CE thì các đường trung trực của DE luôn đi qua 1 điểm cố định M
Cho tam giác ABC vuông tại A (AB < AC). Tia phân giác của góc B cắt AC tại E. Trên cạnh BC lấy điểm D sao cho DB = AB. Hai đường thẳng AB và DE cắt nhau tại I. Chứng minh:
a) AE= DE
b) ∆AEI = ∆DEC
c) BE ⊥ CI
d) AC > 2DE
giúp mk với
Cho tam giác ABC cân tại A. Các đường trung trực của AB và AC cắt nhau tại O. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho BD CE. Chứng minh:a)
∆
D
O
B
∆
E
O
C
;
b) AO là đường trung trực của DE;c) DE // BC.
Đọc tiếp
Cho tam giác ABC cân tại A. Các đường trung trực của AB và AC cắt nhau tại O. Lấy điểm D thuộc cạnh AB, điểm E thuộc cạnh AC sao cho BD = CE. Chứng minh:
a) ∆ D O B = ∆ E O C ;
b) AO là đường trung trực của DE;
c) DE // BC.
Cho tam giác ABC cân tại A Hai đường trung trực của BC và AB cắt nhau tại M trên cạnh AB lấy điểm D và trên cạnh AC lấy điểm E sao cho AD=CE CMR
MD=ME
Cho tam giác ABC, AB AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD AE. Gọi M là giao điểm của BE và CD. Chứng minh:a) BE CD;b)
∆
B
M
D
∆
C
M
E
;
c) Đường vuông góc với OE tại E cắt Ox, Oy lần lượt tại M, N. Chứng minh MN // AC //BD.
Đọc tiếp
Cho tam giác ABC, AB = AC. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE. Gọi M là giao điểm của BE và CD. Chứng minh:
a) BE = CD;
b) ∆ B M D = ∆ C M E ;
c) Đường vuông góc với OE tại E cắt Ox, Oy lần lượt tại M, N. Chứng minh MN // AC //BD.
Cho tam giác ABC có AB < AC . Trên cạnh AB lấy điểm D , trên cạnh AC lấy điểm E sao cho BD = CE . Đường trung trực của DC và DE cắt nhau ở O
CHỨNG Minh Rằng tam giác BOD = COE