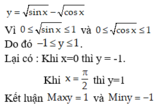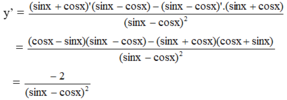Tìm cực trị của các hàm số sau: y = cosx − sinx

Những câu hỏi liên quan
Tìm cực trị của các hàm số sau:
a) y = sin2x
b) y = cosx − sinx
c) y = sin 2 x
a) y = sin2x
Hàm số có chu kỳ T = π
Xét hàm số y=sin2x trên đoạn [0;π], ta có:
y' = 2cos2x
y' = 0 ⇔ 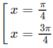
Bảng biến thiên:
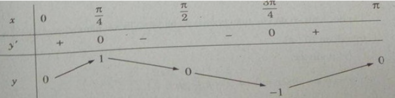
Do đó trên đoạn [0;π] , hàm số đạt cực đại tại π/4 , đạt cực tiểu tại 3π/4 và y C D = y(π/4) = 1; y C T = y(3π/4) = −1
Vậy trên R ta có:
y C Đ = y(π/4 + kπ) = 1;
y C T = y(3π/4 + kπ) = −1, k∈Z
b) Hàm số tuần hoàn chu kỳ nên ta xét trên đoạn [−π;π].
y′ = − sinx – cosx
y′ = 0 ⇔ tanx = −1 ⇔ x = −π4 + kπ, k∈Z
Lập bảng biến thiên trên đoạn [−π;π]
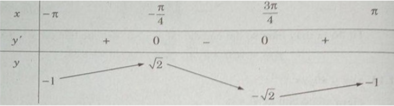
Hàm số đạt cực đại tại x = −π4 + k2π , đạt cực tiểu tại x = 3π4 + k2π (k∈Z) và
y C Đ = y(−π4 + k2π) = 2 ;
y C T = y(3π4 + k2π) = − 2 (k∈Z).
c) Ta có:
![]()
Do đó, hàm số đã cho tuần hoàn với chu kỳ π.
Ta xét hàm số y trên đoạn [0;π]:
![]()
y′ = sin2x
y′ = 0 ⇔ sin2x = 0 ⇔ x = kπ/2 (k∈Z)
Lập bảng biến thiên trên đoạn [0,π]
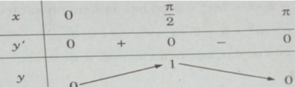
Từ đó, ta thấy hàm số đạt cực tiểu tại x = kπ/2 với k chẵn, đạt cực đại tại x = kπ/2 với k lẻ, và
y C T = y(2mπ) = 0; yCT = y(2mπ) = 0;
y C Đ = y((2m+1)π/2) = 1 (m∈Z)
Đúng 0
Bình luận (0)
Áp dụng Quy tắc 2, hãy tìm các điểm cực trị của hàm số sau: y = sinx + cosx
TXĐ: D = R
+ y’ = cos x – sin x.
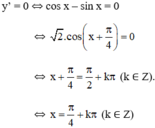
+ y’’ = -sin x – cos x = 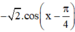
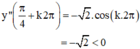
⇒ 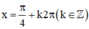 là các điểm cực đại của hàm số.
là các điểm cực đại của hàm số.
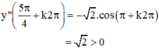
⇒ 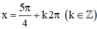 là các điểm cực tiểu của hàm số.
là các điểm cực tiểu của hàm số.
Đúng 0
Bình luận (0)
tìm cực trị của hàm số sau
y=sinx-cosx
ta tính \(y'=cosx+sinx=\sqrt{2}cos\left(x-\frac{\Pi}{4}\right)\)
giải pt y'=0 ta có
\(\sqrt{2}cos\left(x-\frac{\Pi}{4}\right)=0\Rightarrow x-\frac{\Pi}{4}=\frac{\Pi}{2}+k\Pi\Rightarrow x=\frac{3\Pi}{4}+k\Pi\)
ta tình \(y''=-sinx+cosx\)
ta có \(y''\left(\frac{-\Pi}{4}\right)=\sqrt{2}>0\)hàm số đạt cực tiểu tại x\(\frac{-\Pi}{4}+2k\Pi\)
ta có \(y''\left(\frac{3\Pi}{4}\right)=-\sqrt{2}
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau y
sinx
-
cos
x
A: max y 1; min y
-
1
2
B: max y 1; min y -1 C: max y 1; min y 0 D: Đáp án khác
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số sau y = sinx - cos x
A: max y = 1; min y = - 1 2
B: max y = 1; min y = -1
C: max y = 1; min y = 0
D: Đáp án khác
Tìm hoành độ các điểm cực đại
x
C
Đ
; hoành độ các điểm cực tiểu
x
C
T
của đồ thị hàm số ysinx+cosx
Đọc tiếp
Tìm hoành độ các điểm cực đại x C Đ ; hoành độ các điểm cực tiểu x C T của đồ thị hàm số y=sinx+cosx
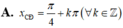
![]()
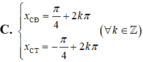
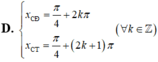
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau:
y=sinx - cosx -sin2x + 1
y=2( sinx + cosx )+4 sinx.cosx - 2
Tìm đạo hàm của các hàm số sau y = sin x + cos x sin x - c o s x
1/ tìm TXĐ chủa hàm số y = căn 1 - cosx /2 + sinx.
2/ tìm tập giá trị của hàm số y = 2-cos2x.
3/ Tìm giá trị lớn nhất và nhỏ nhất của các hàm số sau :
a) y=1 + 2sinx b)y=1 - 2cos^2x
4/ Tìm giá trị nhỏ nhất của hàm số y=tan^2x - 2tanx +3.
1. Không dịch được đề
2.
\(-1\le cos2x\le1\Rightarrow1\le y\le3\)
3.
a. \(-2\le2sinx\le2\Rightarrow-1\le y\le3\)
\(y_{min}=-1\) khi \(sinx=-1\Rightarrow x=-\dfrac{\pi}{2}+k2\pi\)
\(y_{max}=3\) khi \(sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b.
\(0\le cos^2x\le1\Rightarrow-1\le y\le2\)
\(y_{min}=-1\) khi \(cos^2x=1\Rightarrow x=k\pi\)
\(y_{max}=2\) khi \(cosx=0\Rightarrow x=\dfrac{\pi}{2}+k\pi\)
4.
\(y=\left(tanx-1\right)^2+2\ge2\)
\(y_{min}=2\) khi \(tanx=1\Rightarrow x=\dfrac{\pi}{4}+k\pi\)
Đúng 0
Bình luận (0)
Dùng đồ thị hàm số, tìm giá trị của x trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\) để:
a) Hàm số y = sinx nhận giá trị bằng 1
b) Hàm số y = sinx nhận giá trị bằng 0
c) Hàm số y = cosx nhận giá trị bằng – 1
d) Hàm số y = cosx nhận giá trị bằng 0
a) Hàm số y = sinx nhận giá trị bằng 1
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 1
- Lấy giao điểm của hai hàm số y = sinx và y = 1 là A, B,...
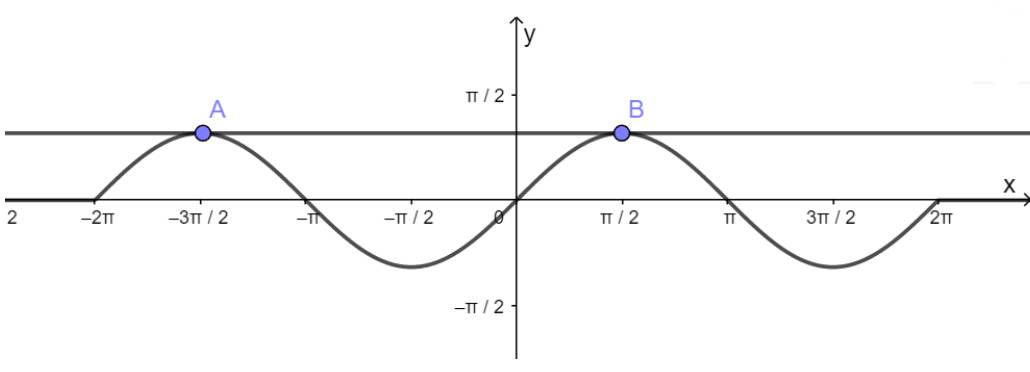
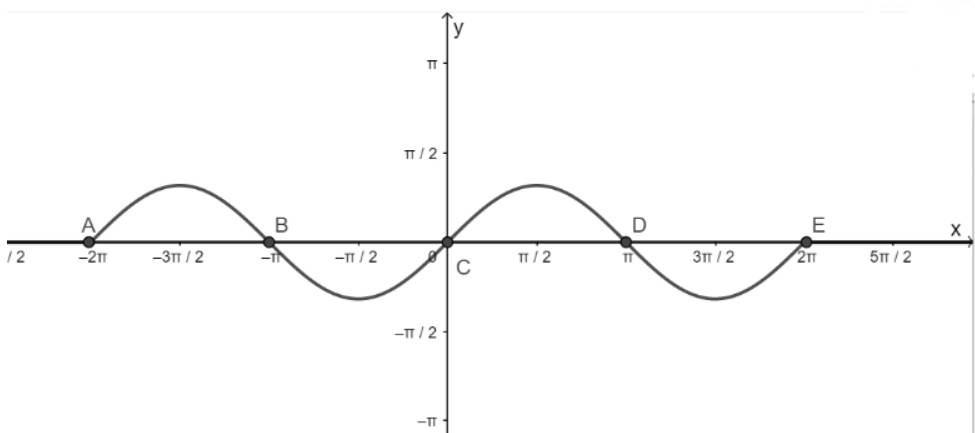
b) Hàm số y = sinx nhận giá trị bằng 0
- Vẽ hàm số y = sinx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = sinx và y = 0 là A, B, C, D, E,...
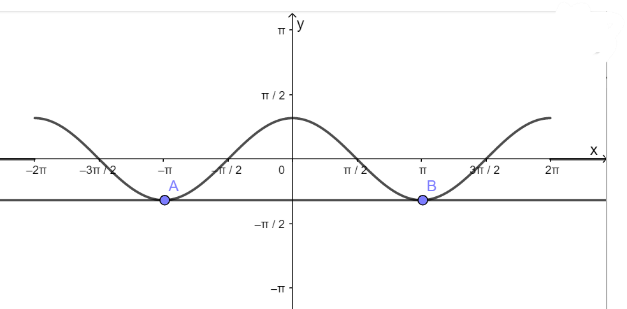
c) Hàm số y = cosx nhận giá trị bằng – 1
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = - 1
- Lấy giao điểm của hai hàm số y = cosx và y = - 1 là A, B,...
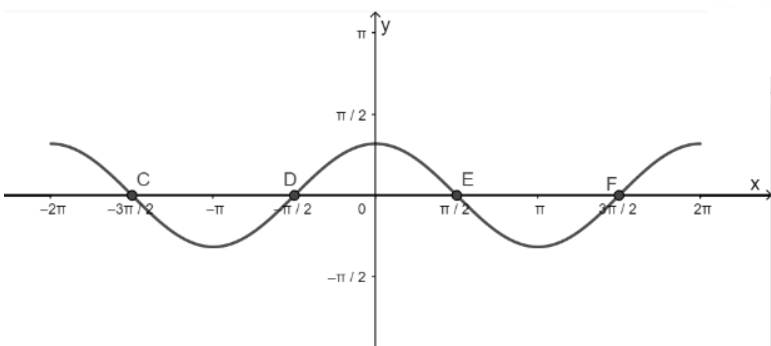
d) Hàm số y = cosx nhận giá trị bằng 0
- Vẽ hàm số y = cosx trên đoạn \(\left[ { - 2\pi ;2\pi } \right]\)
- Vẽ hàm số y = 0
- Lấy giao điểm của hai hàm số y = cosx và y = 0 là C, D, E, F,...
Đúng 0
Bình luận (0)