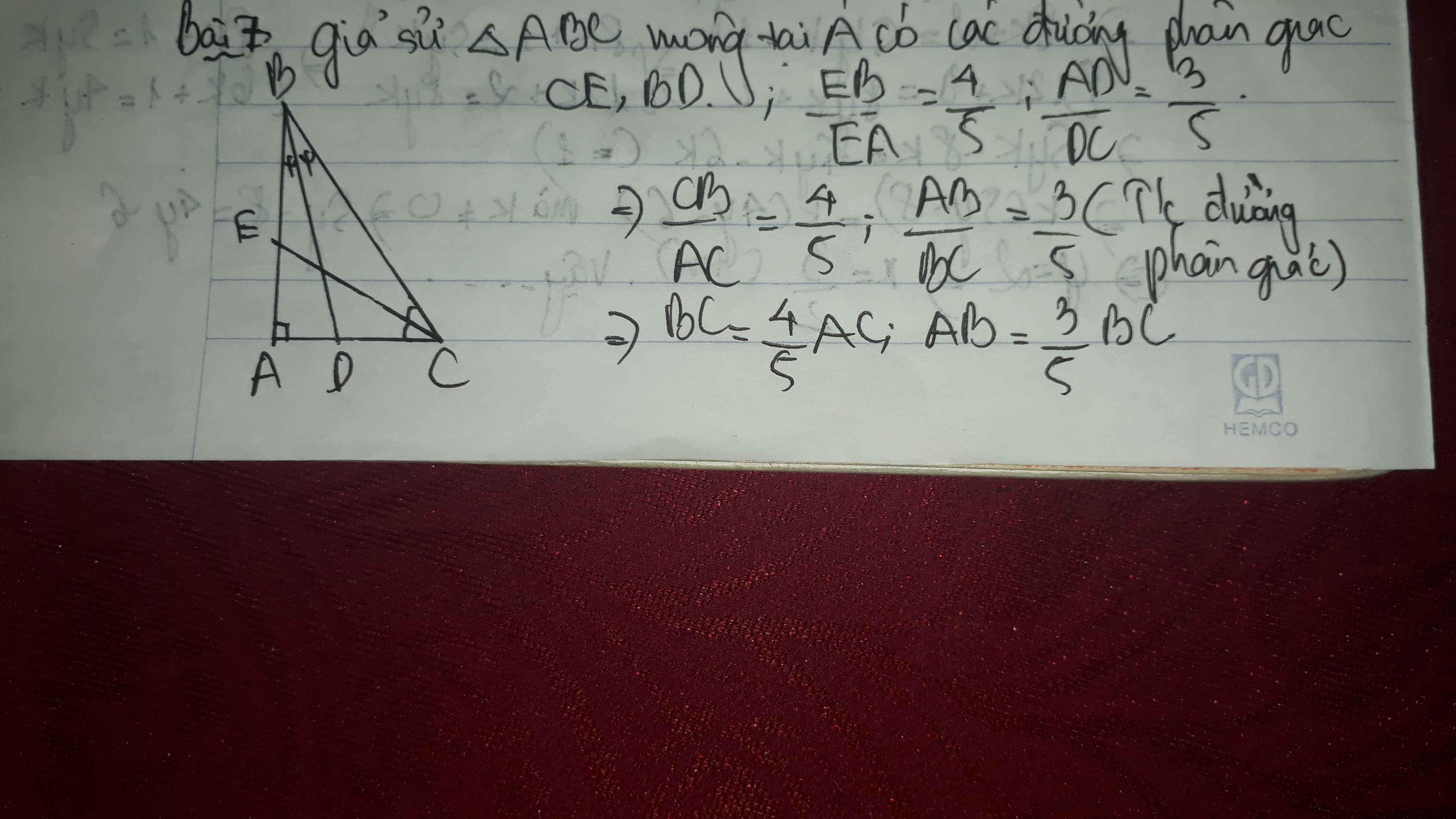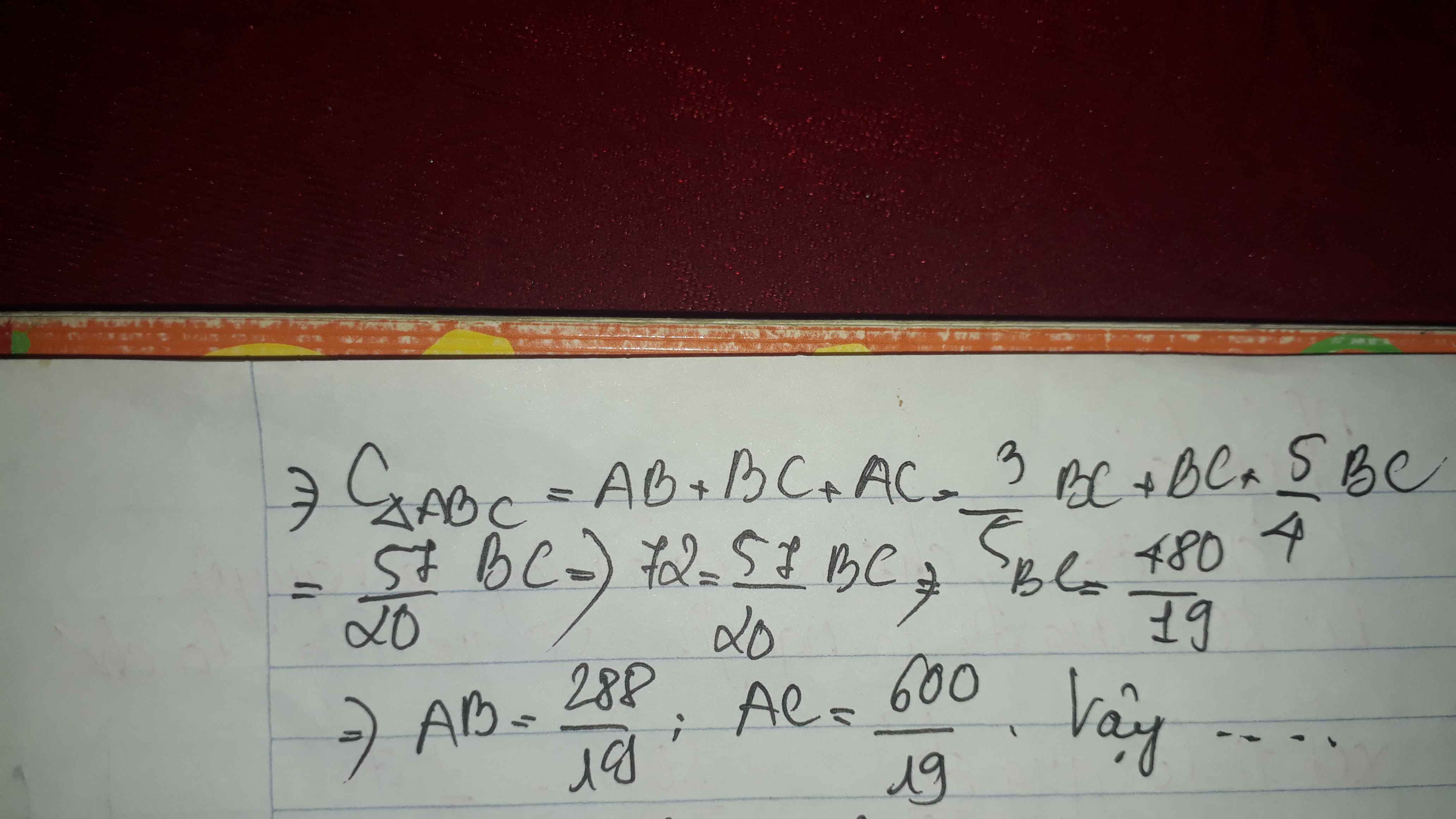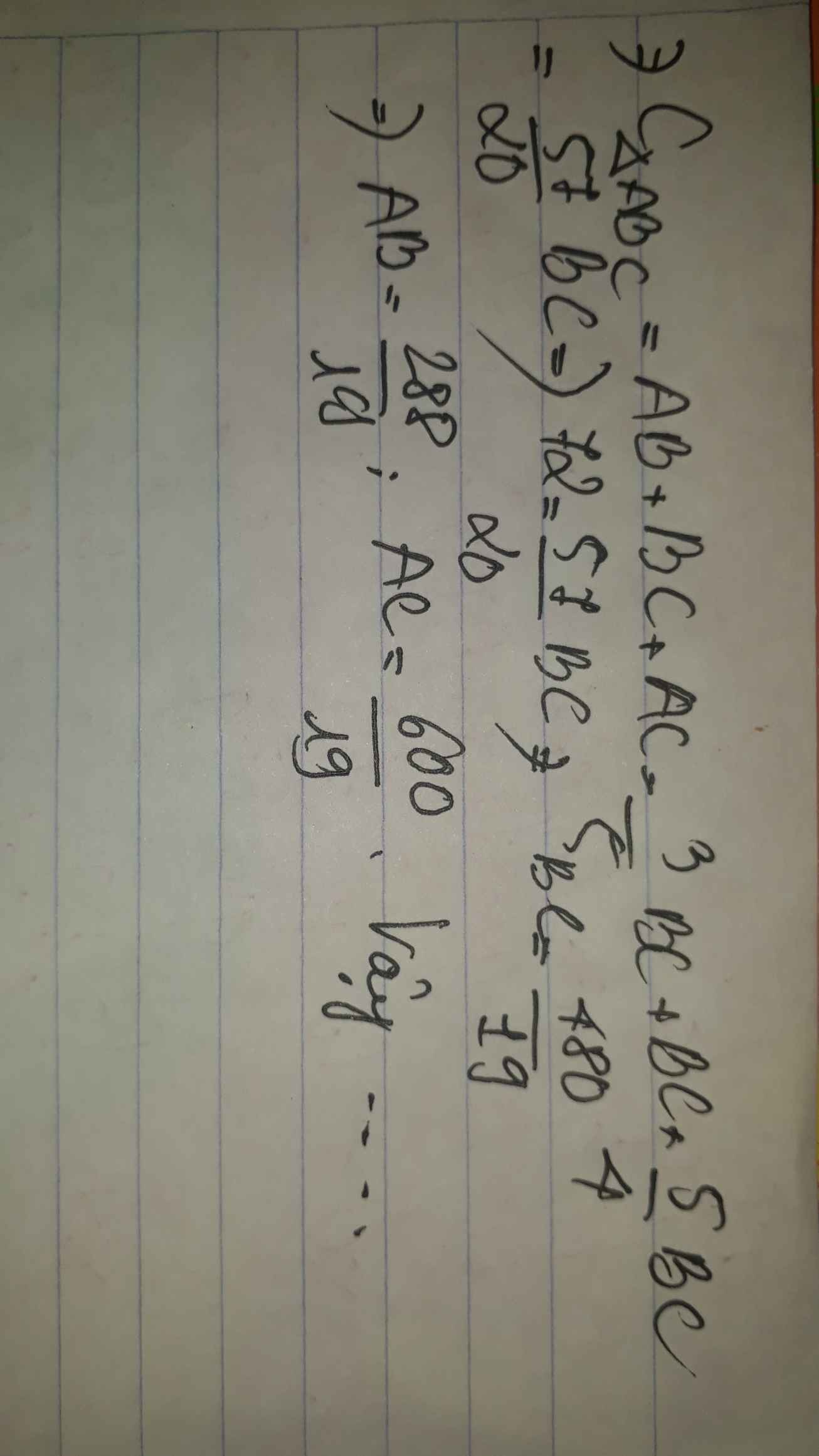Bài 1: Biết các cạnh của một tam giác tỉ lệ với 2;3;5 và chu vi của nó bằng 45cm.
Tính các cạnh của tam giác đó

Những câu hỏi liên quan
BÀI 1 tính chu vi của một tam giác,biết tổng độ dài 2 cạnh nhỏ hơn cạnh lớn 4 cm,các cạnh của tam giác tỉ lệ với các số 3,4,5
BÀI 2 tìm số đo mỗi 3 góc của tam giác lần lượt tỉ lệ với 1:2:3
BÀI 1 : chia số 12 thành 4 phần tỉ lệ với các số 3 ; 5 ; 7 và 9 .
BÀI 2 : các cạnh của một tam giác có số đo tỉ lệ với các số 3 ; 5 ; 7 tính mỗi cạnh của tam giác đó , biết chu vi của bằng 40,5 m .
Bài 1:
Gọi 4 phần đó lần lượt là a, b, c, d.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{3}=\frac{b}{5}=\frac{c}{7}=\frac{d}{9}=\frac{a+b+c+d}{3+5+7+9}=\frac{12}{24}=\frac{1}{2}\)
\(\frac{a}{3}=\frac{1}{2}\Rightarrow a=\frac{3}{2}\)
\(\frac{b}{5}=\frac{1}{2}=\Rightarrow b=\frac{5}{2}\)
\(\frac{c}{7}=\frac{1}{2}\Rightarrow c=\frac{7}{2}\)
\(\frac{d}{9}=\frac{1}{2}\Rightarrow d=\frac{9}{2}\)
Bài 2:
Gọi mỗi cạnh của tam giác lần lượt là:x (cm) , y (cm) , z (cm) và x , y , z phải là số dương.
Ta có : \(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}\) và \(x+y+z=40,5\)
Áp dụng tính chất của dãy tỉ số bằng nhau:
\(\frac{x}{3}=\frac{y}{5}=\frac{z}{7}=\frac{x+y+z}{3+5+7}=\frac{40,5}{15}=2,7\)
\(\frac{x}{3}=2,7.3=8,1\frac{y}{5}=2,7.5=13,5\frac{z}{7}=2,7.7=18,9\)
Vậy mỗi cạnh của tam giác lần lượt là: \(8,1;13,5;18,9\)
Bài 4. Tính số đo các cạnh của một tam giác biết các cạnh của nó tỉ lệ với các số 2: 4: 5 và chu vi tam giác là 44cm.Bài 5. Cho biết x và y là 2 đại lượng tỉ lệ thuận với nhau và khi x 6 thì y 3 a/ Hãy tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo xb/ Tính giá trị của y khi x - 4: x 10Bài 6. (bổ sung) Cho biết x và y là 2 đại lượng tỉ lệ nghịch với nhau và khi x 5 thì y 8 a/ Hãy tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x b/ Tính giá trị của y khi x 4: x 20Bài 7. Tam giác...
Đọc tiếp
Bài 4. Tính số đo các cạnh của một tam giác biết các cạnh của nó tỉ lệ với các số 2: 4: 5 và chu vi tam giác là 44cm.
Bài 5. Cho biết x và y là 2 đại lượng tỉ lệ thuận với nhau và khi x = 6 thì y = 3 a/ Hãy tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x
b/ Tính giá trị của y khi x = - 4: x = 10
Bài 6. (bổ sung) Cho biết x và y là 2 đại lượng tỉ lệ nghịch với nhau và khi x = 5 thì y = 8 a/ Hãy tìm hệ số tỉ lệ của y đối với x và biểu diễn y theo x b/ Tính giá trị của y khi x = 4: x = 20
Bài 7. Tam giác ABC có số đo các góc A, B, C lần lượt tỉ lệ với 3, 5, 7. Tính số đo các góc của tam giác ABC, biết tổng số đo ba góc của một tam giác bằng 1800.
Bài 8. Để giúp các bạn học sinh vùng bị lũ lụt ba lớp 7A, 7B, 7C đã quyên góp được 375 quyển vở để ủng hộ. Biết lớp 7A có 31 học sinh, lớp 7B có 26 học sinh và lớp 7C có 18 học sinh. Tìm số quyển vở của mỗi lớp đã quyên góp biết rằng số quyển vở tỉ lệ với số học sinh của mỗi lớp.
Bài 4:
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{44}{11}=4\)
Do đó: a=8; b=16; c=20
Đúng 1
Bình luận (0)
1)tính độ dài các cạnh của một tam giác biết chu vi là 22 cm các cạnh của tam giác tỉ lệ với 2;3;4
2)tìm các góc của 1 tam giác biết tổng số đo các góc của nó ty lệ với 2;3;4 ?
1) bạn sai đề rồi phải tỉ lệ với 2;4;5 cơ mik làm rồi hjhj
gọi độ dài các cạnh đó lần lượt là a;b;c
=>a/2=b/4=c/5
áp dug t/c dãy t/s = nhua ta có:
a/2=b/4=c/5=a+b+c/2+4+5=22/11=2
=>a/2=2=>a=4
=>b/4=2=>b=8
=>c/5=2=>c=10
Đúng 0
Bình luận (0)
Bài 1: Tính độ dài các cạnh của một tam giác, biết chu vi là 22 cm và các cạnh của tam giác tỉ lệ với các số 2;4;5
Bài 2: Tính số học sinh của lớp 7/1 và lớp 7/2, biết rằng số học sinh lớp 7/1 ít hơn số học sinh lớp 7/2 là 5 học sinh và tỉ số học sinh của hai lớp là 8:9
Bài 1:
Gọi độ dài 3 cạnh tam giác là a,b,c (a,b,c>0; a,b,c<22)
Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{22}{11}=2\)
\(\dfrac{a}{2}=2\Rightarrow a=4\\ \dfrac{b}{4}=2\Rightarrow b=8\\ \dfrac{c}{5}=2\Rightarrow c=10\)
Bài 2:
Gọi số học sinh của lớp 7/1 và lớp 7/2 lần lượt là a,b,c(a,b,c>0)
Áp dụng t/c dtsbn ta có:
\(\dfrac{a}{8}=\dfrac{b}{9}=\dfrac{b-a}{9-8}=\dfrac{5}{1}=5\)
\(\dfrac{a}{8}=5\Rightarrow a=40\\ \dfrac{b}{9}=5\Rightarrow b=45\)
Đúng 1
Bình luận (0)
a.tam giác ABC có độ dài cạnh tỉ lệ với 4,5,7 . Tính độ dài cạnh của tam giác biết chu vi của tam giác lớn hơn 2 lần cạnh nhỏ nhất là 2 cm
b. Tính độ dài các cạnh của 1 tam giác biết chu vi là 33cm và các cạnh của tam giác tỉ lệ với các số 2,4,5
a: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có: a/4=b/5=c/7 và a+b+c-2a=2
Áp dụng tính chất của DTBSN, ta được:
\(\dfrac{a}{4}=\dfrac{b}{5}=\dfrac{c}{7}=\dfrac{a+b+c-2a}{4+5+7-2\cdot4}=\dfrac{2}{8}=\dfrac{1}{4}\)
=>a=1; b=5/4; c=7/4
b: Gọi độ dài ba cạnh lần lượt là a,b,c
Theo đề, ta có:
a/2=b/4=c/5
Áp dụng tính chất của DTSBN, ta đc:
\(\dfrac{a}{2}=\dfrac{b}{4}=\dfrac{c}{5}=\dfrac{a+b+c}{2+4+5}=\dfrac{33}{11}=3\)
=>a=6; b=12; c=15
Đúng 0
Bình luận (0)
Bài 7 : trong 1 tam giác vuông, phân giác của góc nhọn chia cạnh đối diện thành 2 phần tỉ lệ với 4:5 và 3:5 . Biết chu vi tam giác bằng 72. Tính các cạnh của tam giác đó?Bài 8: trong 1 tam giác vuông, phân giác của góc vuông chia cạnh huyền thành 2 phần có độ dài 1cm và 3cm. Hỏi đường cao tương ứng với cạnh huyền theo tỉ số nào ?Bài 9: Tam giác ABC vuông tại A, đường phân giác BD.Tia phân giác của góc A cắt BD ở I. Biết IB10sqrt{5}cm; ID 5sqrt{5}cm, tính diện tích tam giác ABC.
Đọc tiếp
Bài 7 : trong 1 tam giác vuông, phân giác của góc nhọn chia cạnh đối diện thành 2 phần tỉ lệ với 4:5 và 3:5 . Biết chu vi tam giác bằng 72. Tính các cạnh của tam giác đó?
Bài 8: trong 1 tam giác vuông, phân giác của góc vuông chia cạnh huyền thành 2 phần có độ dài 1cm và 3cm. Hỏi đường cao tương ứng với cạnh huyền theo tỉ số nào ?
Bài 9: Tam giác ABC vuông tại A, đường phân giác BD.Tia phân giác của góc A cắt BD ở I. Biết IB=\(10\sqrt{5}\)cm; ID= \(5\sqrt{5}\)cm, tính diện tích tam giác ABC.
Bài 7 : trong 1 tam giác vuông, phân giác của góc nhọn chia cạnh đối diện thành 2 phần tỉ lệ với 4:5 và 3:5 . Biết chu vi tam giác bằng 72. Tính các cạnh của tam giác đó?Bài 8: trong 1 tam giác vuông, phân giác của góc vuông chia cạnh huyền thành 2 phần có độ dài 1cm và 3cm. Hỏi đường cao tương ứng với cạnh huyền theo tỉ số nào ?Bài 9: Tam giác ABC vuông tại A, đường phân giác BD.Tia phân giác của góc A cắt BD ở I. Biết IB10√5cm; ID 5√5cm, tính diện tích tam giác ABC.
Đọc tiếp
Bài 7 : trong 1 tam giác vuông, phân giác của góc nhọn chia cạnh đối diện thành 2 phần tỉ lệ với 4:5 và 3:5 . Biết chu vi tam giác bằng 72. Tính các cạnh của tam giác đó?
Bài 8: trong 1 tam giác vuông, phân giác của góc vuông chia cạnh huyền thành 2 phần có độ dài 1cm và 3cm. Hỏi đường cao tương ứng với cạnh huyền theo tỉ số nào ?
Bài 9: Tam giác ABC vuông tại A, đường phân giác BD.Tia phân giác của góc A cắt BD ở I. Biết IB=10√5cm; ID= 5√5cm, tính diện tích tam giác ABC.
Với hình học bạn lưu ý chỉ nên đăng 1 bài 1 post. Đăng thế này khả năng bị bỏ qua bài rất cao, vì ai nhìn vào cũng thấy nản.
Đúng 0
Bình luận (1)
Độ dài các cạnh của một tam giác tỉ lệ với nhau như thế nào , biết nếu cộng lần lượt độ dài từng 2 đường cao của tam giác đó thì các tổng này tỉ lệ theo 3:4:5
giải thanh bài giúp tôi
gọi độ dài của 3 cạnh của tam giác là a,b,c . Độ dài 3 đường cao tương ứng là x,y,z
ta có: x+y:y+z:x+z = 3:4:5
=> x+y/3 = y+z/4= x+z/5 = k
=> x+y = 3k
=> y+z = 4k
=> x+z = 5k
=> 2.(x+y+z) = 12k
=> x+y+z = 6k
..............................
Đúng 0
Bình luận (0)
à 14 – x = 1 à x = 13 ; khi ®ã = 2000 à Plín nhÊt = 2001.
Gäi ®é dµi c¸c c¹nh tam gi¸c lµ a, b, c ; c¸c ®êng cao t¬ng øng víi c¸c c¹nh ®ã lµ ha , hb , hc .
Ta cã: (ha +hb) : ( hb + hc ) : ( ha + hc ) = 3 : 4 : 5
Hay: (ha +hb) = ( hb + hc ) =( ha + hc ) = k ,( víi k 0).
Suy ra: (ha +hb) = 3k ; ( hb + hc ) = 4k ; ( ha + hc ) = 5k .
Céng c¸c biÓu thøc trªn, ta cã: ha + hb + hc = 6k.
Tõ ®ã ta cã: ha = 2k ; hb =k ; hc = 3k.
MÆt kh¸c, gäi S lµ diÖn tÝch , ta cã:
a.ha = b.hb =c.hc
a.2k = b.k = c.3k
Đúng 0
Bình luận (0)