Rút gọn rồi tính giá trị các biểu thức sau: - 9 a - 9 + 12 a + 4 a 2 t ạ i a = - 9

Những câu hỏi liên quan
Rút gọn rồi tính giá trị các biểu thức sau:
a
)
−
9
a
−
9
+
12
a
+
4
a
2
t
a
i
...
Đọc tiếp
Rút gọn rồi tính giá trị các biểu thức sau:
a ) − 9 a − 9 + 12 a + 4 a 2 t a i a = − 9 b ) 1 + 3 m m − 2 m 2 − 4 m + 4 tai m = 1 , 5 c ) 1 − 10 a − 25 a 2 − 4 a t a i a = 2 d ) 4 x − 9 x 2 + 6 x + 1 t a i x = − 3
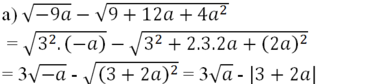
Tại a = -9 ta được:
= 3√-(-9) - |3 + 2(-9)|
= 3√32 - |3 - 18|
= 3.3 - |-15| = 9 - 15 = -6
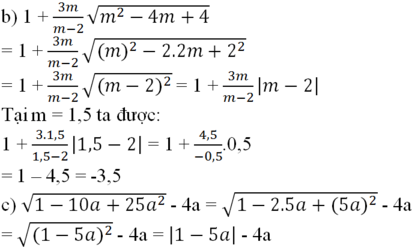
Tại a = √2 ta được:
= |1 - 5√2| - 4√2
= (5√2 - 1) - 4√2
= √2 - 1
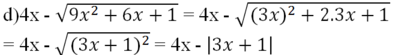
Tại x = -√3 ta được:
= 4(-√3) - |3(-√3) + 1|
= -4√3 - |-3√3 + 1|
= -4√3 - (3√3 - 1)
= -7√3 + 1
Đúng 0
Bình luận (0)
Rút gọn rồi tính giá trị các biểu thức sau: 1 - 10 a - 25 a 2 - 4 a t ạ i a = 2
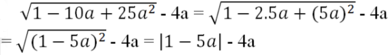
Tại a = √2 ta được:
= |1 - 5√2| - 4√2
= (5√2 - 1) - 4√2
= √2 - 1
Đúng 0
Bình luận (0)
rút gọn các biểu thức sau rồi tính giá trị biểu thức
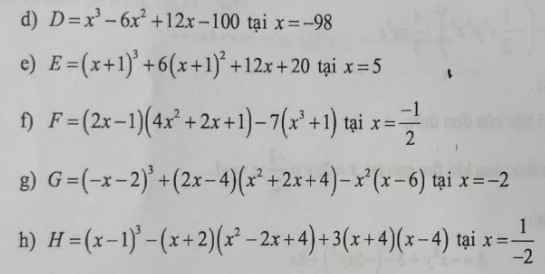
d: \(D=x^3-6x^2+12x-100\)
\(=x^3-6x^2+12x-8-92\)
\(=\left(x-2\right)^3-92\)
Khi x=-98 thì \(D=\left(-98-2\right)^3-92=-1000000-92=-1000092\)
e: \(E=\left(x+1\right)^3+6\left(x+1\right)^2+12x+20\)
\(=\left(x+1\right)^3+6\left(x+1\right)^2+12\left(x+1\right)+8\)
\(=\left(x+1+2\right)^3\)
\(=\left(x+3\right)^3\)
Khi x=5 thì \(E=\left(5+3\right)^3=8^3=512\)
f: \(F=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=x^3-8\)
Khi x=-1/2 thì \(F=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)
g: \(G=\left(-x-2\right)^3+\left(2x-4\right)\left(x^2+2x+4\right)-x^2\left(x-6\right)\)
\(=-\left(x+2\right)^3+2\left(x-2\right)\left(x^2+2x+4\right)-x^3+6x^2\)
\(=-x^3-6x^2-12x-8+2\left(x^3-8\right)-x^3+6x^2\)
\(=-2x^3-12x-8+2x^3-16=-12x-24\)
Khi x=-2 thì \(G=-12\cdot\left(-2\right)-24=24-24=0\)
h: \(H=\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)+3\left(x+4\right)\left(x-4\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+8\right)+3\left(x^2-16\right)\)
\(=x^3-3x^2+3x-1-x^3-8+3x^2-48\)
\(=3x-57\)
Khi x=-1/2 thì \(H=3\cdot\dfrac{-1}{2}-57=-1,5-57=-58,5\)
Đúng 1
Bình luận (0)
1 a. Rút gọn biểu thức sau A = \(\left(x^{\text{2}}-2x+4\right):\left(x^3+8\right)-x^2\) rồi tính giá trị của A tại x = -2
b. Rút gọn biểu thức B = (x - 2) : 2x + 5x rồi tính giá trị của biểu thức B tại x = 0
C1
A= 25x-25-9x-9+ √x-1
a, Tìm điều kiện để A có nghĩa
b,Rút gọn A
c, Tìm x để A=12
C2
Cho biểu thức: P=3x- √x^2 - 10x+25
a, Rút gọn biểu thức
b, Tính giá trị của P khi x=2
Câu 2:
a: Ta có: \(P=3x-\sqrt{x^2-10x+25}\)
\(=3x-\left|x-5\right|\)
\(=\left[{}\begin{matrix}3x-x+5=2x+5\left(x\ge5\right)\\3x+x-5=4x-5\left(x< 5\right)\end{matrix}\right.\)
b: Vì x=2<5 nên \(P=4\cdot2-5=8-5=3\)
Đúng 0
Bình luận (0)
Câu 1 (1,5 điểm). Cho các biểu thức A = 2√x +1/√x -3 và
B =2x+36/x-9 - 9/√x -3 - √x/√x +3 (với x≥0;x≠ 9)
a) Tính giá trị của A khi x = 49
b) Rút gọn biểu thức B.
c) Đặt P = A.B. Tìm tất cả các giá trị của x để P > 1.
a: Thay x=49 vào A, ta được:
\(A=\dfrac{2\cdot7+1}{7-3}=\dfrac{14+1}{4}=\dfrac{15}{4}\)
b: \(B=\dfrac{2x+36}{x-9}-\dfrac{9}{\sqrt{x}-3}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{2x+36}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}-\dfrac{9}{\sqrt{x}-3}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{2x+36-9\left(\sqrt{x}+3\right)-\sqrt{x}\left(\sqrt{x}-3\right)}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{2x+36-9\sqrt{x}-27-x+3\sqrt{x}}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}\)
\(=\dfrac{x-6\sqrt{x}+9}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{\left(\sqrt{x}-3\right)^2}{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\)
c: \(P=A\cdot B=\dfrac{\sqrt{x}-3}{\sqrt{x}+3}\cdot\dfrac{2\sqrt{x}+1}{\sqrt{x}-3}=\dfrac{2\sqrt{x}+1}{\sqrt{x}+3}\)
P>1 khi P-1>0
=>\(\dfrac{2\sqrt{x}+1-\sqrt{x}-3}{\sqrt{x}+3}>0\)
=>\(\sqrt{x}-2>0\)
=>\(\sqrt{x}>2\)
=>x>4
Kết hợp ĐKXĐ, ta được: \(\left\{{}\begin{matrix}x>4\\x\ne9\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Rút gọn rồi tính giá trị biểu thức sau với c = 88:
87 - c + 12
Cho biểu thức: x^2+6x+9/x+3 a) Rút gọn biểu thức A b) Tính giá trị của a tại x=-2
\(a,\dfrac{x^2+6x+9}{x+3}\\ đk:x\ne-3\\ =\dfrac{\left(x+3\right)^2}{x+3}=x+3\)
b, Thay \(x=-2\left(t/mđk\right)\) vào
\(-2+3=1\)
Vậy tại \(x=-2\) thì biểu thức = 1
Đúng 2
Bình luận (1)
\(A=\dfrac{x^2+6x+9}{x+3}\)
\(A=\dfrac{x^2+2.x.3+3^2}{x+3}\)
\(A=\dfrac{\left(x+3\right)^2}{x+3}\)
\(A=x+3\)
b) Thay x = -2 vào A ta được A = -2 + 3 = 1
Vậy khi x = -2 thì A = 1
Đúng 1
Bình luận (2)
\(a)\dfrac{x^2+6x+9}{x+3}=\dfrac{\left(x+3\right)^2}{x+3}=x+3\)
\(\text{b)Thay x=-2 vào biểu thức x+3,ta được:}\)
\(x+3=\left(-2\right)+3=1\)
\(\text{Vậy giá trị của biểu thức trên tại x=-2 là:1}\)
Đúng 0
Bình luận (0)
Rút gọn và tính giá trị các biểu thức sau :
(a-b-c)+(a+b) tại a=-12;b=-14;c=-27
( a - b - c ) + ( a + b )
= a - b - c + a + b
= ( a + a ) + ( -b + b ) - c
= 2a + 0 - c
thay a = -12 , c = -27
=> 2 x -12 + 0 + 27
=> -24 + 27
= 3
vạy bt có giá trị là 3
Đúng 0
Bình luận (0)
Xem thêm câu trả lời





















